题目内容
1. 在正六边形ABCDEF中,P是AB边上一点,PM∥AF交EF于M,PN∥BC交CD于N.
在正六边形ABCDEF中,P是AB边上一点,PM∥AF交EF于M,PN∥BC交CD于N.(1)直接写出$\frac{PM+PN}{ED}$的值为3
(2)若$\frac{PN}{PM}=\frac{5}{4}$,①求证:PB=2PA;②求$\frac{FD}{MN}$的值.
分析 (1)如图1中,作AH∥EF交PM于H,作BG∥CD交PK于G,设AP=a,PB=b,则AF=BC=ED=a+b,求出PM+PN,即可解决问题;
(2)①如图2中,作AH∥EF交PM于H,作BG∥CD交PK于G,设AP=a,PB=b,则AF=BC=a+b,由PN:PM=5:4,可得(a+2b):(2a+b)=5:4,推出4a+8b=10a+5b,推出b=2a即可解决问题;
②如图3中,延长FE交CD的延长线于K,连接DF,作NT⊥EK于T,EW⊥DF于W.设正六边形的边长为6m.求出DF、MN即可解决问题;
解答 (1)解:如图1中,作AH∥EF交PM于H,作BG∥CD交PK于G,设AP=a,PB=b,则AF=BC=ED=a+b,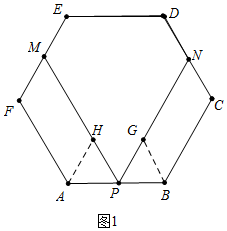
在正六边形ABCDEF中,∠F=∠FAB=∠ABC=∠C=120°
∵PM∥AF交EF于M,PN∥BC交CD于N,
∴四边形MFAH、四边形BCKG是平行四边形,易证△APH,△PBG是等边三角形,
∴HM=AF,GJ=BC,PH=PA=a,PG=PB=b,
∴PM+PK=a+b+a+a+b+b=3(a+b),
∴$\frac{PM+PN}{ED}$=$\frac{3(a+b)}{a+b}$=3.
故答案为3.
(2)①证明:如图2中,作AH∥EF交PM于H,作BG∥CD交PK于G,设AP=a,PB=b,则AF=BC=a+b,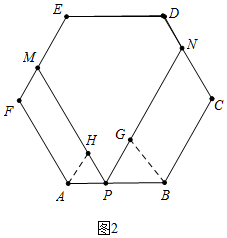
易知:PM=2a+b,PN=a+2b,
∵PN:PM=5:4,
∴(a+2b):(2a+b)=5:4,
∴4a+8b=10a+5b,
∴b=2a,
∴PB=2PA.
②如图3中,延长FE交CD的延长线于K,连接DF,作NT⊥EK于T,EW⊥DF于W.设正六边形的边长为6m.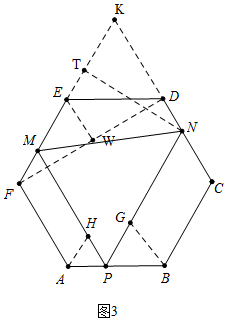
由(2)可知PA=2m,PB=4m,易知EM=4m,DN=2m,EM=10m,KN=8m,
在Rt△KNT中,∵∠NTK=90°,∠K=60°,
∴TK=$\frac{1}{2}$KN=4m,TN=4$\sqrt{3}$m,
在Rt△MTN中,∵∠MTN=90°,TM=6m,
∴MN=$\sqrt{T{M}^{2}+T{N}^{2}}$=$\sqrt{(6m)^{2}+(4\sqrt{3}m)^{2}}$=2$\sqrt{21}$m,
在Rt△EFW中,FW=EF•cos30°=3$\sqrt{3}$m,
∵EF=ED,EW⊥DF,
∴FW=WD,
∴DF=6$\sqrt{3}$m,
∴$\frac{FD}{MN}$=$\frac{6\sqrt{3}m}{2\sqrt{21}m}$=$\frac{3\sqrt{7}}{7}$.
点评 本题考查正多边形的性质、平行四边形的判定和性质.解直角三角形等知识,解题的关键是学会添加常用辅助线,构造特殊四边形解决问题,学会利用参数解决问题,属于中考压轴题.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案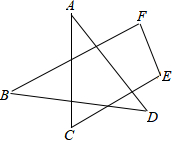 如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数. BD平分∠ABC,CD平分外角∠ACG,DE∥BC交AB于E,交AC于F,线段EF与BE、CF有什么关系?
BD平分∠ABC,CD平分外角∠ACG,DE∥BC交AB于E,交AC于F,线段EF与BE、CF有什么关系?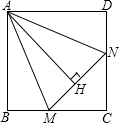 已知,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M、N,AH⊥MN于点H,如图MH=2,NH=3,求AH的长.
已知,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M、N,AH⊥MN于点H,如图MH=2,NH=3,求AH的长.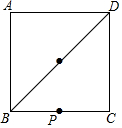 一个正方形的田地,BD所在线段种的是苹梨树,小明家在BC中点P处.他要从家出发摘苹果然后拿到位于点C处的集市上去卖,请在BD上找一点M,使得小明所走路径最短,即PM+CM最短,(要求:尺规作图,不写作法,保留作图痕迹)
一个正方形的田地,BD所在线段种的是苹梨树,小明家在BC中点P处.他要从家出发摘苹果然后拿到位于点C处的集市上去卖,请在BD上找一点M,使得小明所走路径最短,即PM+CM最短,(要求:尺规作图,不写作法,保留作图痕迹) 如图,直线y=-x+3与x轴,y轴分别相交于点B,C,经过B,C两点的抛物线y=ax2+bx+c与x轴的另一交点为A,顶点为P,且对称轴是直线x=2.
如图,直线y=-x+3与x轴,y轴分别相交于点B,C,经过B,C两点的抛物线y=ax2+bx+c与x轴的另一交点为A,顶点为P,且对称轴是直线x=2.