题目内容
1.解方程组:$\left\{{\begin{array}{l}{x-z=-5}\\{x+y=7}\\{z-y=8}\end{array}}\right.$.分析 ①+③得出x-y=3④,由④和②组成二元一次方程组$\left\{\begin{array}{l}{x-y=3}\\{x+y=7}\end{array}\right.$,求出x、y的值,把x=5代入①求出z即可.
解答 解:$\left\{\begin{array}{l}{x-z=-5①}\\{x+y=7②}\\{z-y=8③}\end{array}\right.$
①+③得:x-y=3④,
由④和②组成方程组$\left\{\begin{array}{l}{x-y=3}\\{x+y=7}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=5}\\{y=2}\end{array}\right.$,
把x=5代入①得:5-z=-5,
解得:z=10,
所以原方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=2}\\{z=10}\end{array}\right.$.
点评 本题考查了三元一次方程组,能把三元一次方程组转化成二元一次方程组是解此题的关键.

练习册系列答案
相关题目
11.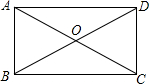 如图,在矩形ABCD中,对角线AC与BD相交于点O,AC=8,∠BOC=120°,则矩形的面积是( )
如图,在矩形ABCD中,对角线AC与BD相交于点O,AC=8,∠BOC=120°,则矩形的面积是( )
 如图,在矩形ABCD中,对角线AC与BD相交于点O,AC=8,∠BOC=120°,则矩形的面积是( )
如图,在矩形ABCD中,对角线AC与BD相交于点O,AC=8,∠BOC=120°,则矩形的面积是( )| A. | 16 | B. | 32 | C. | 8$\sqrt{3}$ | D. | 16$\sqrt{3}$ |
9.在平面直角坐标系中,如果点P(a,b)到y轴的距离为2,那么( )
| A. | a=2 | B. | a=±2 | C. | b=2 | D. | b=±2 |
16.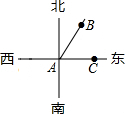 已知A、B两地的位置如图所示,且∠BAC=60°,那么下列语句正确的是( )
已知A、B两地的位置如图所示,且∠BAC=60°,那么下列语句正确的是( )
 已知A、B两地的位置如图所示,且∠BAC=60°,那么下列语句正确的是( )
已知A、B两地的位置如图所示,且∠BAC=60°,那么下列语句正确的是( )| A. | A地在B地的北偏东60°方向 | B. | A地在B地的北偏东30°方向 | ||
| C. | B地在A地的北偏东60°方向 | D. | B地在A地的北偏东30°方向 |
 如图,在△ABC中,∠90°.
如图,在△ABC中,∠90°.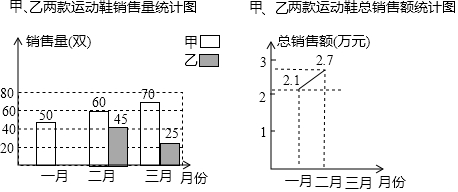
 △ABC与△A′B′C′关于直线l对称,则∠B的度数为105°.
△ABC与△A′B′C′关于直线l对称,则∠B的度数为105°.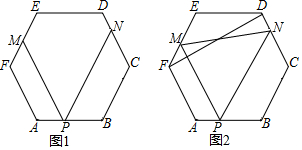 在正六边形ABCDEF中,P是AB边上一点,PM∥AF交EF于M,PN∥BC交CD于N.
在正六边形ABCDEF中,P是AB边上一点,PM∥AF交EF于M,PN∥BC交CD于N.