题目内容
11. △ABC中,D是AC上一点,AD:DC=2:1,BD=$\sqrt{3}$+1,∠ADB=60°,∠C=45°,试判断直线AB与△BCD的外接圆是相交还是相切,并证明你的结论.
△ABC中,D是AC上一点,AD:DC=2:1,BD=$\sqrt{3}$+1,∠ADB=60°,∠C=45°,试判断直线AB与△BCD的外接圆是相交还是相切,并证明你的结论.
分析 过B作BE⊥AD,E为垂足,不妨设AD=2,CD=1,设ED=x,由∠C=45°,∠ADB=60°,可得到$\sqrt{3}$x=x+1,求出x,利用勾股定理可求出AB=6,因此得到AB2=AD•AC,△ABD∽△ACB,∠ABD=∠ACB=45°,再证明∠ABF=90°,过B作直径BF即可得到.
解答 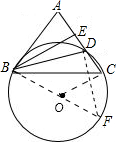 解:直线AB与△BCD的外接圆相切.
解:直线AB与△BCD的外接圆相切.
理由:如图,⊙O为△BCD的外接圆.过B作BE⊥AD,E为垂足,不妨设AD=2,CD=1,设ED=x,
∵∠C=45°,
∴BE=x+1,
∵∠ADB=60°,
∴BE=$\sqrt{3}$DE=$\sqrt{3}$x,即$\sqrt{3}$x=x+1,
∴x=$\frac{\sqrt{3}+1}{2}$,
则BE=$\frac{3+\sqrt{3}}{2}$,AE=AD-ED=2-x=$\frac{3-\sqrt{3}}{2}$,
在RT△AEB中,AB2=BE2+AE2=($\frac{3+\sqrt{3}}{2}$)2+($\frac{3-\sqrt{3}}{2}$)2=6,
而AD•AC=2×3=6
∴AB2=AD•AC,而∠A公共,
∴△ABD∽△ACB,
∴∠ABD=∠ACB=45°,
过B作直径BF,则∠ADF=90°,
连DF,则∠F=∠ACB=45°,
∴∠DBF=45°,
∴∠ABF=90°,
∴AB是⊙O的切线,即AB是△BCD的外接圆的切线.
点评 本题考查了直线与圆的位置关系,根据题意作出△BCD的外接圆,构造出直角三角形,利用勾股定理求解是解答此题的关键.

练习册系列答案
相关题目
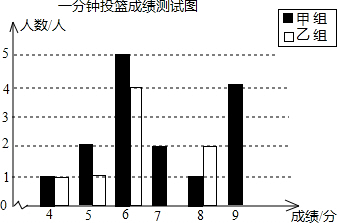
2.一分钟投篮测试规定,得6分以上为合格,得9分以上为优秀,甲、乙两组同学的一次测试成绩如下:
(1)请你根据上述统计数据,把下面的图和表补充完整.
(2)下面是小明和小聪的一段对话.请你根据(1)中的表,写出两条支持小聪的观点的理由.
小明:我认为,因为甲组的优秀率高于乙组,所以甲组的成绩更好于乙组;
小聪:我认为:乙组的成绩要好于甲组.
| 成绩(分) | 4 | 5 | 6 | 7 | 8 | 9 |
| 甲组(人) | 1 | 2 | 5 | 2 | 1 | 4 |
| 乙组(人) | 1 | 1 | 4 | 5 | 2 | 2 |

| 统计量 | 平均分 | 方差 | 中位数 | 合格率 | 优秀率 |
| 甲组 | 6.8 | 2.56 | 6 | 80.0% | 26.7% |
| 乙组 | 6.8 | 1.76 | 7 | 86.7% | 13.3% |
小明:我认为,因为甲组的优秀率高于乙组,所以甲组的成绩更好于乙组;
小聪:我认为:乙组的成绩要好于甲组.
19.2014年12月30日,晋豫鲁铁路正式开通运营,据了解,晋豫鲁铁路是“晋煤外运”的新通道.线路起自山西兴县瓦塘站,终点是山东日照,全线长1260公里,横跨山西、河南、山东三省.总投资941亿元,941亿用科学记数法表示为( )
| A. | 941×108 | B. | 94.1×109 | C. | 9.41×1010 | D. | 9.41×1011 |
16.用配方法解方程x2-4x+1=0时,原方程可以变形为( )
| A. | (x+2)2=3 | B. | (x-2)2=4 | C. | (x-2)2=3 | D. | (x-2)2=15 |
 等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P;
等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P; 如图,已知半圆A的面积是3,半圆B的面积是4,则半圆C的面积是7.
如图,已知半圆A的面积是3,半圆B的面积是4,则半圆C的面积是7.