题目内容
8. 如图,在Rt△ABC中∠ACB=90°,CD⊥AB于D
如图,在Rt△ABC中∠ACB=90°,CD⊥AB于D(1)求证:△ADC∽△CDB;
(2)若AD=2,BD=6,求CD的长.
分析 (1)利用等角的余角相等得到∠B=∠ACD,则利用有两组角对应相等的两三角形相似可判断△ADC∽△CDB;
(2)利用相似比得到$\frac{AD}{CD}$=$\frac{CD}{BD}$,然后利用比例性质求CD.
解答 (1)证明:∵CD⊥AB于D,
∴∠CDA=∠CDB=90°,
∴∠BCD+∠B=90°
∵∠ACB=90°,即∠BCD+∠ACD=90°,
∴∠B=∠ACD,
∴△ADC∽△CDB;
(2)解:∵△ADC∽△CDB,
∴$\frac{AD}{CD}$=$\frac{CD}{BD}$,即$\frac{2}{CD}$=$\frac{CD}{6}$,
∴CD=2$\sqrt{3}$.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用;再运用相似三角形的性质时主要利用相似比进行几何计算.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
19.下列说法正确的是( )
| A. | 垂线段就是垂直于已知直线的线段 | |
| B. | 垂线段就是垂直于已知直线并且与已知直线相交的线段 | |
| C. | 垂线段是一条竖起来的线段 | |
| D. | 过直线外一点向该直线作垂线,这一点到垂足之间的线段叫垂线段 |

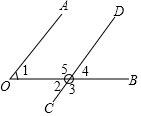 如图,直线CD与∠AOB的边OB相交.
如图,直线CD与∠AOB的边OB相交. 如图,在Rt△ABC中,∠ACB=90°,CH⊥AB于点H,若BC=5,AC=12,则AB=13,CH=$\frac{60}{13}$.
如图,在Rt△ABC中,∠ACB=90°,CH⊥AB于点H,若BC=5,AC=12,则AB=13,CH=$\frac{60}{13}$. 实数x在数轴上的位置如图所示,试化简:|x+2|-$\sqrt{(-x)^{2}}$-2$\sqrt{9-6x+{x}^{2}}$.
实数x在数轴上的位置如图所示,试化简:|x+2|-$\sqrt{(-x)^{2}}$-2$\sqrt{9-6x+{x}^{2}}$. ,0)、(3
,0)、(3 ,0)、(0,5),点D在第一象限,且∠ADB=60º,则线段CD的长的最小值为______.
,0)、(0,5),点D在第一象限,且∠ADB=60º,则线段CD的长的最小值为______.