题目内容
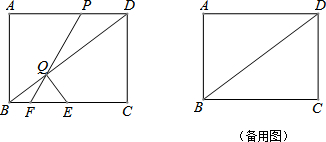
10.如图,在矩形ABCD中,已知AB=3,BC=4,连接BD,动点P从点D出发向终点A运动,同时动点Q从点B出发向点D运动,速度均为1个单位/秒.当其P点到达终点A时,点Q随即停止.过点Q作BD的垂线交折线B-C-D于点E,射线PQ交折线B-C-D于点F.设运动时间为t秒.(1)当点E在BC边上时,用含t的代数式表示BE的长;
(2)当t=2时,求线段BF的长;
(3)若以点F为圆心,FQ的长度为半径的⊙F经过点E时,求t的值;
(4)作线段EF关于BD的轴对称变换得到线段E′F′,当四边形EFF′E′为矩形时,请直接写出t的值.
分析 (1)根据题意证明△BQE∽△BCD,根据相似三角形的性质得到成比例线段,代入已知数据求值即可;
(2)t=2时,求出BQ、QD的值,根据△PQD∽△FQB得到成比例线段,代入求值即可;
(3)从点F、E都在BC上、点F、E都在CD上和点E在BC上,点F在CD上三种情况根据相似三角形的性质进行分析解答;
(4)根据当EF∥BD时,四边形EFF′E′为矩形解答即可.
解答 解:(1)∵在矩形ABCD中,CD=AB=3,BC=4,
∴BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=5,
∵QE⊥BD,
∴∠BQE=∠C=90°,
又∵∠QBE=∠CBD,
∴△BQE∽△BCD,
∴$\frac{BE}{BD}$=$\frac{BQ}{BC}$,即 $\frac{BE}{5}$=$\frac{t}{4}$,
∴BE=$\frac{5}{4}$t;
(2)当t=2秒,BQ=PD=2,QD=3,
由△PQD∽△FQB,得:$\frac{BF}{2}$=$\frac{2}{3}$,
∴BF=$\frac{4}{3}$;
(3)①点F、E都在BC上时,若FQ=EF,则易证FE=BF,
即BE=$\frac{1}{2}$×$\frac{5}{4}$t=$\frac{5}{8}$t,
由△PQD∽△FQB,得:$\frac{PD}{BF}$=$\frac{QD}{QB}$,
即$\frac{t}{\frac{5}{8}t}$=$\frac{5-t}{t}$,
解得,t=$\frac{25}{13}$
②点F、E都在CD上时,同理可得FE=FD,
如图1,过点P作PG∥AB交BD于G,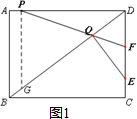
由△QDF∽△QPG得:$\frac{DF}{PG}$=$\frac{QD}{QG}$,
即$\frac{\frac{5}{6}(5-t)}{\frac{3}{4}t}$=,
解得,t=$\frac{100}{27}$,
当点E在BC上,点F在CD上时,显然FQ>FE;
综上所述,当⊙F经过点E时,t=$\frac{25}{13}$或t=$\frac{100}{27}$;
(4)如图2,当EF∥BD时,四边形EFF′E′为矩形,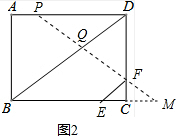
$\frac{PD}{MB}$=$\frac{DQ}{BQ}$,即MB=$\frac{{t}^{2}}{5-t}$,
$\frac{CM}{PD}=\frac{CF}{DF}=\frac{CE}{BE}$,
即$\frac{4-\frac{{t}^{2}}{5-t}}{t}=\frac{4-\frac{5}{4}t}{\frac{5}{4}t}$,
解得,t=$\frac{180}{61}$
点评 本题考查的是矩形的性质、相似三角形的判定和性质以及勾股定理的运用,正确运用分情况讨论思想和数形结合思想是解题的关键,注意运用运动的观点解决问题.

| 采购数量(件) | 1 | 2 | … |
| A产品单价(元/件) | 250 | 230 | … |
| B产品单价(元/件) | 130 | 120 | … |
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的$\frac{1}{3}$,且A产品采购单价不低于100元,求该商家共有几种进货方案;
(3)该商家分别以300元/件和150元/件的销售单价售出A,B两种产品,且全部售完,在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润.
 如图,OA是北偏东30°方向的一条射线,若射线OB与射线OA垂直,则OB的方向角是( )
如图,OA是北偏东30°方向的一条射线,若射线OB与射线OA垂直,则OB的方向角是( )| A. | 西偏北30° | B. | 北偏西60° | C. | 北偏东30° | D. | 东偏北60° |
 如图,已知等边△ABC,以AB为直径的圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连结GD.
如图,已知等边△ABC,以AB为直径的圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连结GD. 如图,四边形ABCD内接于⊙O,AD∥BC,P为BD上一点,∠APB=∠BAD.
如图,四边形ABCD内接于⊙O,AD∥BC,P为BD上一点,∠APB=∠BAD. 如图,已知点A(-1,3),点B(-3,0),AC⊥y轴,求四边形ABOC的面积.
如图,已知点A(-1,3),点B(-3,0),AC⊥y轴,求四边形ABOC的面积.