题目内容
5.为迎接国际动漫节,某商家计划从厂家采购A,B两种类型的cosplay服装共20件,衣服的采购单价(元/件)是采购数量(件)的一次函数,下表提供了部分采购数据.| 采购数量(件) | 1 | 2 | … |
| A产品单价(元/件) | 250 | 230 | … |
| B产品单价(元/件) | 130 | 120 | … |
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的$\frac{1}{3}$,且A产品采购单价不低于100元,求该商家共有几种进货方案;
(3)该商家分别以300元/件和150元/件的销售单价售出A,B两种产品,且全部售完,在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润.
分析 (1)设y1与x的关系式y1=kx+b,利用待定系数法,求出k和b的值,函数关系式即可求出;
(2)首先根据题意列出不等式组,求出x的取值范围,结合x为整数,即可判断出商家的几种进货方案;
(3)分别计算出两种方案的利润,即可解答.
解答 解:(1)y1与x的关系式y1=kx+b,
把(1,250),(2,230)代入得:$\left\{\begin{array}{l}{k+b=250}\\{2k+b=230}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=-20}\\{b=270}\end{array}\right.$
∴y1=-20x+270.
(2)由题意得:$\left\{\begin{array}{l}{x≥\frac{1}{3}(20-x)}\\{-20x+270≥100}\end{array}\right.$
解得5≤x≤8.5,
又∵A、B产品得单价要大于零,
∴$\left\{\begin{array}{l}{-20x+270>0}\\{-10(20-x)+140>0}\end{array}\right.$
解得:6<x<13.5,
综合得6<x≤8.5,
答:有两种进货方案:A产品7件,B产品13件或者A产品8件,B产品12件.
(3)当x=7时,总利润=7×(300-130)+13×(150-10)=3010,
当x=8时,总利润=8×(300-110)+12×(150-20)=3080
当x=8时,利润最大,最大利润为3080元.
点评 本题考查了一元一次不等式组及一次函数的应用,将现实生活中的事件与数学思想联系起来,读懂题列出关系式是解题的关键.

练习册系列答案
相关题目
16.下列运算正确的是( )
| A. | (a3)2=a5 | B. | ($\frac{1}{2}$a3b)2=$\frac{1}{4}$a6b2 | C. | (-x-y)2=x2-2xy+y2 | D. | (-a-b)(a+b)=a2-b2 |
17.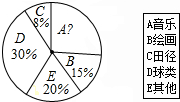 某初中为了了解初中学生课余时间最喜欢的文体活动,学生会在本校初中学生中随机调查了部分学生最喜欢的文体活动项目:A音乐,B绘画,C田径,D球类,E其他(被调查对象选且只选其中的一项),对调查结果进行整理,并制作了不完整的统计表和统计图(如图所示):
某初中为了了解初中学生课余时间最喜欢的文体活动,学生会在本校初中学生中随机调查了部分学生最喜欢的文体活动项目:A音乐,B绘画,C田径,D球类,E其他(被调查对象选且只选其中的一项),对调查结果进行整理,并制作了不完整的统计表和统计图(如图所示):
“最喜欢的文体活动”调查统计表
(1)根据统计表和图中的信息将“统计表”填写完整;
(2)若该校共有初中学生900人,请你估计该校最喜欢“A音乐”的人数约有多少人?
 某初中为了了解初中学生课余时间最喜欢的文体活动,学生会在本校初中学生中随机调查了部分学生最喜欢的文体活动项目:A音乐,B绘画,C田径,D球类,E其他(被调查对象选且只选其中的一项),对调查结果进行整理,并制作了不完整的统计表和统计图(如图所示):
某初中为了了解初中学生课余时间最喜欢的文体活动,学生会在本校初中学生中随机调查了部分学生最喜欢的文体活动项目:A音乐,B绘画,C田径,D球类,E其他(被调查对象选且只选其中的一项),对调查结果进行整理,并制作了不完整的统计表和统计图(如图所示):“最喜欢的文体活动”调查统计表
| 项目 | A音乐 | B绘画 | C田径 | D球类 | E其他 |
| 频数 | 正正正正正正 | ||||
| 人数(人) | 20 |
(2)若该校共有初中学生900人,请你估计该校最喜欢“A音乐”的人数约有多少人?
18.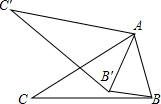 如图所示,在△ABC中,∠CAB=70°,现将△ABC绕点A顺时针旋转一定角度后得到△AB′C′,连接BB′,若BB′∥AC′,则∠CAB′的度数为( )
如图所示,在△ABC中,∠CAB=70°,现将△ABC绕点A顺时针旋转一定角度后得到△AB′C′,连接BB′,若BB′∥AC′,则∠CAB′的度数为( )
 如图所示,在△ABC中,∠CAB=70°,现将△ABC绕点A顺时针旋转一定角度后得到△AB′C′,连接BB′,若BB′∥AC′,则∠CAB′的度数为( )
如图所示,在△ABC中,∠CAB=70°,现将△ABC绕点A顺时针旋转一定角度后得到△AB′C′,连接BB′,若BB′∥AC′,则∠CAB′的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 40° |
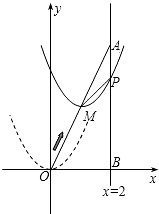 如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连接OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.
如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连接OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.



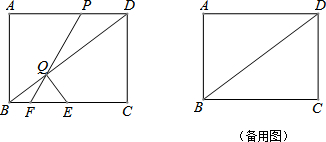
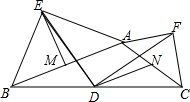 如图,在钝角△ABC中,分别以AB和AC为斜边向△ABC的外侧作等腰直角三角形ABE和等腰直角三角形ACF,EM平分∠AEB交AB于点M,取BC中点D,AC中点N,连接DN、DE、DF.下列结论:①EM=DN;②S△CDN=$\frac{1}{3}$S四边形ABDN;③DE=DF;④DE⊥DF.其中正确的结论的个数是( )
如图,在钝角△ABC中,分别以AB和AC为斜边向△ABC的外侧作等腰直角三角形ABE和等腰直角三角形ACF,EM平分∠AEB交AB于点M,取BC中点D,AC中点N,连接DN、DE、DF.下列结论:①EM=DN;②S△CDN=$\frac{1}{3}$S四边形ABDN;③DE=DF;④DE⊥DF.其中正确的结论的个数是( )