题目内容
18. 如图,已知等边△ABC,以AB为直径的圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连结GD.
如图,已知等边△ABC,以AB为直径的圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连结GD.(1)求证:DF是⊙O的切线;
(2)若AB=12,求FG的长;
(3)在(2)问条件下,求点D到FG的距离.
分析 (1)连接OD,证∠ODF=90°即可.
(2)利用△CDF是30°的直角三角形可求得CF长,同理可利用△FGA中的60°的三角函数值可求得FG长.
(3)过D作DH⊥AB于H.利用△BDH是30°的直角三角形可求得BH长,同理可求得AG,然后根据GH=AB-AG-BH求得即可.
解答 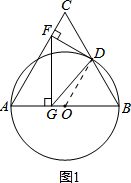 (1)证明:连结OD,如图1,
(1)证明:连结OD,如图1,
∵△ABC为等边三角形,
∴∠C=∠A=∠B=60°.
而OD=OB,
∴△ODB是等边三角形,∠ODB=60°,
∴∠ODB=∠C,
∴OD∥AC,
∵DF⊥AC,
∴OD⊥DF,
∴DF是⊙O的切线.
(2)解:∵OD∥AC,点O为AB的中点,
∴OD为△ABC的中位线.
∴BD=CD=6.
在Rt△CDF中,∠C=60°,
∴∠CDF=30°,
∴CF=$\frac{1}{2}$CD=3.
∴AF=AC-CF=12-3=9,
在Rt△AFG中,∵∠A=60°,
∴FG=AF×sinA=9×$\frac{\sqrt{3}}{2}$=$\frac{9\sqrt{3}}{2}$.
(3)解:如图2,过D作DH⊥AB于H.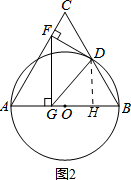
∵FG⊥AB,DH⊥AB,
∴FG∥DH,
在Rt△BDH中,∠B=60°,
∴∠BDH=30°,
∴BH=$\frac{1}{2}$BD=3,DH=$\sqrt{3}$BH=3$\sqrt{3}$.
在Rt△AFG中,∵∠AFG=30°,
∴AG=$\frac{1}{2}$AF=$\frac{9}{2}$,
∵GH=AB-AG-BH=12-$\frac{9}{2}$-3=$\frac{9}{2}$,FG⊥AB,
∴点D到FG的距离是$\frac{9}{2}$.
点评 本题主要考查了切线的判定与性质,等边三角形的性质,30°的直角三角形的性质,解直角三角形等知识.判断直线和圆的位置关系,一般要猜想是相切,再证直线和半径的夹角为90°即可.注意利用特殊的三角形和三角函数来求得相应的线段长.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 10cm | B. | 20cm | C. | 22cm | D. | 24cm |
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
①b=-4;
②存在这样一个a,使得M、A、C三点在同一条直线上;
③抛物线的对称轴位于y轴的右侧;
④若a=1,则3OA•OB=OC2.
正确的有( )
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
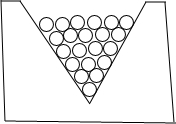 如图所示是工厂里一种统计圆柱形产品(如铅笔)的计数器,工人师傅只要数一数最上层有多少支,就能很快算出产品的总数.
如图所示是工厂里一种统计圆柱形产品(如铅笔)的计数器,工人师傅只要数一数最上层有多少支,就能很快算出产品的总数.(1)请观察计数器模型,填写下表:
| 最上层的产品数(支) | 1 | 2 | 3 | 4 | … | 10 | … |
| 产品总数 | 1 | 3 | 6 | 10 | … | 55 | … |
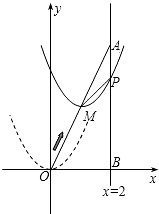 如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连接OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.
如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连接OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.