题目内容
12．已知关于x的方程x2-3x+1=0的两个根为x1、x2，则x1+x2-x1x2=2．分析 根据根与系数的关系可得出“x1+x2=-$\frac{b}{a}$=3，x1•x2=$\frac{c}{a}$=1”，将其代入x1+x2-x1x2中即可得出结论．
解答 解：∵关于x的方程x2-3x+1=0的两个根为x1、x2，
∴x1+x2=-$\frac{b}{a}$=3，x1•x2=$\frac{c}{a}$=1，
∴x1+x2-x1x2=3-1=2．
故答案为：2．
点评 本题考查了根与系数的关系，解题的关键是找出“x1+x2=3，x1•x2=1”．本题属于基础题，难度不大，解决该题型题目时，根据根与系数的关系找出两根之和与两根之积是关键．
练习册系列答案
相关题目
3．假设你班有男生24名，女生26名，班主任要从班里任选一名“社区服务”志愿者，则选中男生的概率是（ ）
| A． | $\frac{12}{25}$ | B． | $\frac{13}{25}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{50}$ |
20．$\frac{1}{2}$sin60°的值等于（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{{\sqrt{3}}}{4}$ | D． | $\sqrt{3}$ |
7．
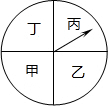如图，将一个可以自由旋转的转盘等分成甲、乙、丙、丁四个扇形区域，若指针固定不变，转动这个转盘一次（如果指针指在等分线上，那么重新转动，直至指针指在某个扇形区域内为止），则指针指在丙区域内的概率是（ ）
如图，将一个可以自由旋转的转盘等分成甲、乙、丙、丁四个扇形区域，若指针固定不变，转动这个转盘一次（如果指针指在等分线上，那么重新转动，直至指针指在某个扇形区域内为止），则指针指在丙区域内的概率是（ ）| A． | 1 | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{4}$ |
如图，在菱形ABCD中，DE⊥AB，cosA=$\frac{3}{5}$，AE=3，则tan∠DBE的值是2．
2．下列各式中与$\sqrt{12}$是同类二次根式的是（ ）
| A． | $\sqrt{6}$ | B． | $\sqrt{32}$ | C． | $\sqrt{18}$ | D． | $\sqrt{75}$ |