��Ŀ����
6�� ��ͼ����A��˫����y=$\frac{8}{x}$��x��0���ϵĶ��㣬��A��AB��x�ᣬAC��y�ᣬ�ֱ�˫����y=$\frac{2}{x}$��x��0���ڵ�B��C������BC�����A�ĺ�����Ϊa��
��ͼ����A��˫����y=$\frac{8}{x}$��x��0���ϵĶ��㣬��A��AB��x�ᣬAC��y�ᣬ�ֱ�˫����y=$\frac{2}{x}$��x��0���ڵ�B��C������BC�����A�ĺ�����Ϊa����1�����ú�a�Ĵ���ʽ�ֱ��ʾA��B��C���ֱ꣨��д������
��2�����ŵ�A���˶�����ABC������Ƿ����仯�������䣬�����ABC����������ı䣬��˵�����ɣ�
��3����ֱ��y=2x���Ƿ���ڵ�D��ʹ�õ�A��B��C��DΪ������ı�����ƽ���ı��Σ������ڣ������Ӧ�ĵ�A���ꣻ�������ڣ���˵�����ɣ�
���� ��1����x=a����˫����y=$\frac{8}{x}$��x��0�������y��ֵ����ʾ��A���ꣻ����A��B��������ͬȷ����B���꣬����A��C��������ͬȷ����C���꼴�ɣ�
��2�����䣬����Ϊ�����ݣ�1����ʾ����AB��AC����ʾ��������ABC��������������жϣ�
��3����ֱ��y=2x�ϴ��ڵ�D��ʹ�õ�A��B��C��DΪ������ı�����ƽ���ı��Σ�������������ǣ��ٵ��ı���ACBDΪƽ���ı��Σ��ڵ��ı���ACDBΪƽ���ı��Σ��۵��ı���ABCDΪƽ���ı��Σ��ֱ����A�����꼴�ɣ�
��� �⣺��1����������ã�A��a��$\frac{8}{a}$����B��$\frac{1}{4}$a��$\frac{8}{a}$����C��a��$\frac{2}{a}$����
��2�����䣬����Ϊ��
��������ã�S��ABC=$\frac{1}{2}$AC•AB=$\frac{1}{2}$•��$\frac{8}{a}$-$\frac{2}{a}$��•��a-$\frac{1}{4}$a��=$\frac{9}{4}$��
�����ŵ�A���˶�����ABC��������䣬���Ϊ$\frac{9}{4}$��
��3����ֱ��y=2x�ϴ��ڵ�D��ʹ�õ�A��B��C��DΪ������ı�����ƽ���ı��Σ�
������������ǣ�
�����ı���ACBDΪƽ���ı��Σ�
��DB=AC��
��$\frac{a}{2}$-$\frac{8}{a}$=$\frac{8}{a}$-$\frac{2}{a}$��
��ã�a=2$\sqrt{7}$��a=-2$\sqrt{7}$��ȥ����
������a=2$\sqrt{7}$��ԭ���̵ĸ���
��A��2$\sqrt{7}$��$\frac{4\sqrt{7}}{7}$����
�����ı���ACDBΪƽ���ı��Σ�
��DC=AB��
��a-$\frac{1}{a}$=a-$\frac{1}{4}$a��
��ã�a=2��a=-2��ȥ����
������a=2��ԭ���̵ĸ���
��A��2��4����
�����ı���ADCBΪƽ���ı��Σ�
��AB=DC��
��a-$\frac{1}{4}$a=$\frac{1}{a}$-a��
��ã�a=$\frac{2\sqrt{7}}{7}$��a=-$\frac{2\sqrt{7}}{7}$��ȥ����
������a=$\frac{2\sqrt{7}}{7}$��ԭ���̵ĸ���
��A��$\frac{2\sqrt{7}}{7}$��4$\sqrt{7}$����
������������A��B��C��DΪ������ı���Ϊƽ���ı���ʱ��A������Ϊ��2$\sqrt{7}$��$\frac{4\sqrt{7}}{7}$����2��4����$\frac{2\sqrt{7}}{7}$��4$\sqrt{7}$����
���� �������ڷ����������ۺ��⣬�漰��֪ʶ�У�������ͼ�����ʣ�������������ͼ�������ʣ�ƽ���ı��ε����ʣ��Լ�������������������շ�����������ͼ���������ǽⱾ��Ĺؼ���

 ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д� ��ͼ���ڡ�ABC�У�AB=AC����O�ڱ�AB�ϣ���O����B�ҷֱ����AB��BC�ཻ�ڵ�D��E��EFΪ��O�����ߣ���AC�ڵ�F��
��ͼ���ڡ�ABC�У�AB=AC����O�ڱ�AB�ϣ���O����B�ҷֱ����AB��BC�ཻ�ڵ�D��E��EFΪ��O�����ߣ���AC�ڵ�F�� ��֪��������y=ax2+bx+c��a��0����ƽ��ֱ������ϵ�е�λ����ͼ����һ�κ���y=ax+b��a��0���뷴��������y=$\frac{c}{x}$��ͬһֱ������ϵ�е�ͼ������ǣ�������
��֪��������y=ax2+bx+c��a��0����ƽ��ֱ������ϵ�е�λ����ͼ����һ�κ���y=ax+b��a��0���뷴��������y=$\frac{c}{x}$��ͬһֱ������ϵ�е�ͼ������ǣ�������


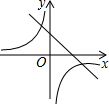
 ��ͼ��������ABCD�У�DE��AB��cosA=$\frac{3}{5}$��AE=3����tan��DBE��ֵ��2��
��ͼ��������ABCD�У�DE��AB��cosA=$\frac{3}{5}$��AE=3����tan��DBE��ֵ��2��



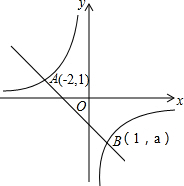 ��ͼ��һ�κ���y=kx+b��ͼ���뷴��������y=$\frac{a}{x}$��ͼ���ཻ��A��B���㣮
��ͼ��һ�κ���y=kx+b��ͼ���뷴��������y=$\frac{a}{x}$��ͼ���ཻ��A��B���㣮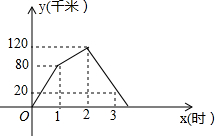 �ס�����������A����B��������ʻ���׳��ȳ�����һ��ʱ����ҳ��ٳ������׳�����B�غ�������ԭ·����һ�ٶ����ٷ��أ�ֱ������������������֮���·��Ϊy��ǧ�ף����׳���ʻ��ʱ��Ϊx��ʱ����y��x֮��ĺ�����ϵͼ����ͼ��ʾ��
�ס�����������A����B��������ʻ���׳��ȳ�����һ��ʱ����ҳ��ٳ������׳�����B�غ�������ԭ·����һ�ٶ����ٷ��أ�ֱ������������������֮���·��Ϊy��ǧ�ף����׳���ʻ��ʱ��Ϊx��ʱ����y��x֮��ĺ�����ϵͼ����ͼ��ʾ��