题目内容
10.如图,在平面直角坐标系中,二次函数y=-$\frac{1}{2}$x2+bx+c的图象与x轴交于点A,B,与y轴交于点C,直线y=-x+4经过B,C两点.(1)求二次函数的解析式;
(2)在BC上方的抛物线上有一动点P.
①如图1,当点P运动到某位置时,以BP,BO为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点P的坐标;
②如图2,过点O,P的直线y=kx交BC于点D,若PD:OD=3:8,求k的值.

分析 (1)根据自变量与函数值的对应关系,可得B,C点坐标,根据待定系数法,可得函数解析式;
(2)①根据平行四边形的对边平行且相等,可得PQ=4,根据函数值相等的点关于对称轴对称,可得P点坐标;
②根据相似三角形的判定与性质,可得PE的长,再根据平行于y轴的直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得关于m的方程,根据解方程,可得m的值,可得P点坐标,根据待定系数法,可得答案.
解答 解:(1)y=-x+4当x=0时,y=4,C点坐标是(0,4),当y=0时,x=4,即B点坐标是(4,0),
将B、C点的坐标代入抛物线,得$\left\{\begin{array}{l}{-\frac{1}{2}×{4}^{2}+4b+c=0}\\{c=4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=1}\\{c=4}\end{array}\right.$,
抛物线的解析式为y=-$\frac{1}{2}$x2+x+4;
(2)①如图1,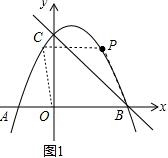
y=-$\frac{1}{2}$x2+x+4的对称轴是x=1,
∵以BP、BO为邻边的平行四边形的第四个顶点Q恰好在抛物线上,
∴PQ∥BO,PQ=BO=4.
∵P,Q都在抛物线上,
∴P,Q关于直线x=1对称,
∴P点的横坐标是3,当x=3时,y=-$\frac{1}{2}$x2+x+4=$\frac{5}{2}$,P点的坐标是(3,$\frac{5}{2}$);
②过P作PE∥OC交BC于点E,如图2,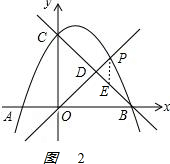
∵PE∥OC,
∴△PDE∽△ODC,
∴$\frac{PD}{OD}$=$\frac{PE}{OC}$,$\frac{PD}{OD}$=$\frac{3}{8}$,OC=4,
∴PE=$\frac{3}{2}$.
设点E的坐标为(m,-m+4),P(m,-$\frac{1}{2}$m2+m+4),
∴-$\frac{1}{2}$m2+m+4-(-m+4)=$\frac{3}{2}$,化简,得
m2-4m+3=0,
解得m1=1,m2=3.
当m=1时,P点坐标是(1,$\frac{9}{2}$),将P点坐标代入解析式,得
k=$\frac{9}{2}$,
当m=3时,P点坐标是(3,$\frac{5}{2}$),将P点坐标代入解析式,得
k=$\frac{5}{6}$,
∴k=$\frac{9}{2}$或k=$\frac{5}{6}$.
点评 本题考查了二次函数综合题,利用待定系数法求函数解析式;利用平行四边的性质得出PQ的长是解题关键,又利用了函数的对称性;利用相似三角形的判定与性质得出关于m的方程是解题关键.

| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{4}$ | D. | $\sqrt{3}$ |
| A. | 130×108 | B. | 1.3×109 | C. | 1.3×1010 | D. | 1.3×1011 |
| A. | $\sqrt{6}$ | B. | $\sqrt{32}$ | C. | $\sqrt{18}$ | D. | $\sqrt{75}$ |
 如图,在菱形ABCD中,DE⊥AB,cosA=$\frac{3}{5}$,AE=3,则tan∠DBE的值是2.
如图,在菱形ABCD中,DE⊥AB,cosA=$\frac{3}{5}$,AE=3,则tan∠DBE的值是2.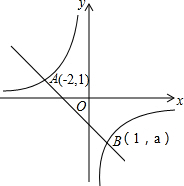 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{a}{x}$的图象相交于A、B两点.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{a}{x}$的图象相交于A、B两点.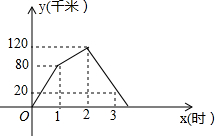 甲、乙两车均由A地向B地匀速行驶,甲车先出发,一段时间后乙车再出发,甲车到达B地后,立即按原路以另一速度匀速返回,直至两车相遇,设两车之间的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数关系图象如图所示.
甲、乙两车均由A地向B地匀速行驶,甲车先出发,一段时间后乙车再出发,甲车到达B地后,立即按原路以另一速度匀速返回,直至两车相遇,设两车之间的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数关系图象如图所示.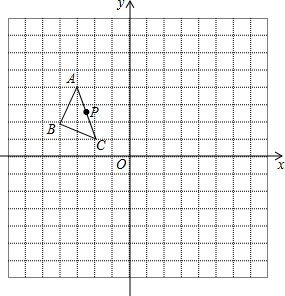 如图,△ABC三个顶点的坐标分别为A(-3,4),B(-4,2),C(-2,1).
如图,△ABC三个顶点的坐标分别为A(-3,4),B(-4,2),C(-2,1).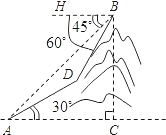 如图,我校九年级一个学习小组进行测量小山高度的实践活动,部分同学在山脚点A测得山腰上一点D的仰角为30°,并测得AD的长度为180米;另一部分同学在山顶点B测得山脚点A的俯角为45°,山腰点D的俯角为60°,请你帮助他们计算出小山BC的高度(结果保留根号).
如图,我校九年级一个学习小组进行测量小山高度的实践活动,部分同学在山脚点A测得山腰上一点D的仰角为30°,并测得AD的长度为180米;另一部分同学在山顶点B测得山脚点A的俯角为45°,山腰点D的俯角为60°,请你帮助他们计算出小山BC的高度(结果保留根号).