题目内容
20.已知$\frac{b+c-a}{a}$=$\frac{c+a-b}{b}$=$\frac{a+b-c}{c}$,则$\frac{a+b+c}{a-b+c}$的值为( )| A. | 3 | B. | 0 | C. | 0或3 | D. | 非上述答案 |
分析 设已知等式等于k,得出三个关系式,结合后化简得到a+b+c=0或k=1,即可确定出原式的值.
解答 解:设$\frac{b+c-a}{a}$=$\frac{c+a-b}{b}$=$\frac{a+b-c}{c}$=k,
可得a+b-c=ck①,a-b+c=bk②,-a+b+c=ak③,
①+②+③得:2(a+b+c)=(k+1)(a+b+c),
整理得:(a+b+c)(2-k-1)=0,
可得a+b+c=0或1-k=0,
若a+b+c=0,可得$\frac{a+b+c}{a-b+c}$=0,
若a+b+c≠0,得k=1,
∴a+b-c=c,a-b+c=b,-a+b+c=a原,
∴a=b=c,
∴原式=$\frac{a+b+c}{b}$=3.
故选C.
点评 此题考查了比例的性质,分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
10.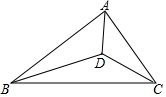 如图,直角三角形ABC中,∠BAC=90°,点D为三角形内部一点,连接AD,BD.CD,AD平分∠BAC,∠BDC=135°,AD=2$\sqrt{2}$,BD=$\sqrt{2}$CD,则BC的长为( )
如图,直角三角形ABC中,∠BAC=90°,点D为三角形内部一点,连接AD,BD.CD,AD平分∠BAC,∠BDC=135°,AD=2$\sqrt{2}$,BD=$\sqrt{2}$CD,则BC的长为( )
 如图,直角三角形ABC中,∠BAC=90°,点D为三角形内部一点,连接AD,BD.CD,AD平分∠BAC,∠BDC=135°,AD=2$\sqrt{2}$,BD=$\sqrt{2}$CD,则BC的长为( )
如图,直角三角形ABC中,∠BAC=90°,点D为三角形内部一点,连接AD,BD.CD,AD平分∠BAC,∠BDC=135°,AD=2$\sqrt{2}$,BD=$\sqrt{2}$CD,则BC的长为( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
5.下列式子一定是二次根式的是( )
| A. | $\sqrt{-x-2}$ | B. | $\sqrt{x}$ | C. | $\sqrt{{x}^{2}+2}$ | D. | $\sqrt{-5}$ |
12.已知一个直角三角形的斜边长是4,一条直角边是3,则第三边长为( )
| A. | 5 | B. | $\sqrt{7}$ | C. | 5或$\sqrt{7}$ | D. | 7 |
9.某市对城区主干道进行绿化,计划把某一段公路的一侧全部栽上桂花树,要求路的两端各栽一棵,并且每两棵树的间隔相等,如果每隔5米栽1棵,则树苗缺21棵;如果每隔6米栽1棵,则树苗正好用完,设原有树苗x棵,则根据题意列出方程正确的是( )
| A. | 5(x+21-1)=6(x-1) | B. | 5(x+21)=6(x-1) | C. | 5(x+21-1)=6x | D. | 5(x+21)=6x |
 如图,在平面直角坐标系中,正比例函数y=2x与反比例函数y=$\frac{k}{x}$(k≠0)相交于A、B两点,已知点A的坐标是(1,a),另有一次函数y=mx+n(m≠0)的图象经过点A,交x轴于点C,交y轴于点D,OC=$\sqrt{5}$OA.
如图,在平面直角坐标系中,正比例函数y=2x与反比例函数y=$\frac{k}{x}$(k≠0)相交于A、B两点,已知点A的坐标是(1,a),另有一次函数y=mx+n(m≠0)的图象经过点A,交x轴于点C,交y轴于点D,OC=$\sqrt{5}$OA.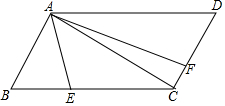 如图,在平行四边形ABCD中,∠B=60°,AC⊥AB,点E在BC上,点F在CD上,满足∠EAF=60°,AE=7,BE:EC=5:11,则DF=6.
如图,在平行四边形ABCD中,∠B=60°,AC⊥AB,点E在BC上,点F在CD上,满足∠EAF=60°,AE=7,BE:EC=5:11,则DF=6.