题目内容
15.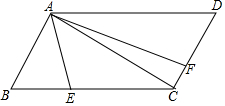 如图,在平行四边形ABCD中,∠B=60°,AC⊥AB,点E在BC上,点F在CD上,满足∠EAF=60°,AE=7,BE:EC=5:11,则DF=6.
如图,在平行四边形ABCD中,∠B=60°,AC⊥AB,点E在BC上,点F在CD上,满足∠EAF=60°,AE=7,BE:EC=5:11,则DF=6.
分析 先过点A作AH⊥BC于H,设BE=5x,EC=11x,得到BH=4x,AH=4$\sqrt{3}$x,HE=x,在Rt△AEH中,由勾股定理可得AH2+HE2=AE2,根据(4$\sqrt{3}$x)2+x2=72,解得x=1,进而得到AH=4$\sqrt{3}$,HE=1,AB=8,AC=8$\sqrt{3}$,再判定△AHE∽△ACF,根据$\frac{AH}{AC}$=$\frac{HE}{CF}$,可得$\frac{4\sqrt{3}}{8\sqrt{3}}$=$\frac{1}{CF}$,即可得到CF=2,再根据DF=CD-CF进行计算即可.
解答 解:如图,过点A作AH⊥BC于H,
设BE=5x,EC=11x,
在Rt△ABC中,∵∠B=60°,
∴∠ACB=30°,
∴AB=$\frac{1}{2}$BC=8x,AC=8$\sqrt{3}$x,
在Rt△ABH中,∵∠B=60°,
∴∠BAH=30°,
∴BH=$\frac{1}{2}$AB=4x,AH=4$\sqrt{3}$x,HE=BE-BH=x,
在Rt△AEH中,由勾股定理可得AH2+HE2=AE2,
即(4$\sqrt{3}$x)2+x2=72,
解得x=1,
∴AH=4$\sqrt{3}$,HE=1,AB=8,AC=8$\sqrt{3}$,
∵平行四边形ABCD中,AB∥CD,AB=CD,
∴∠ACF=∠BAC=∠AHE=90°,CD=8,
∵∠EAF=60°,∠HAC=90°-30°=60°,
∴∠HAE=∠CAF,
又∵∠AHE=∠ACF,
∴△AHE∽△ACF,
∴$\frac{AH}{AC}$=$\frac{HE}{CF}$,即$\frac{4\sqrt{3}}{8\sqrt{3}}$=$\frac{1}{CF}$,
∴CF=2,
∴DF=CD-CF=8-2=6,
故答案为:6.
点评 本题主要考查了平行四边形的性质、含30°角的直角三角形的性质以及相似三角形的判定与性质的运用,解决问题的关键是作辅助线构造相似三角形及直角三角形,依据勾股定理列方程求解,依据相似三角形的对应边成比例进行计算.

 阅读快车系列答案
阅读快车系列答案 如图是婴儿车的平面示意图,其中AB∥CD,∠1=124°,∠3=40°,那么∠2的度数为( )
如图是婴儿车的平面示意图,其中AB∥CD,∠1=124°,∠3=40°,那么∠2的度数为( )| A. | 74° | B. | 76° | C. | 84° | D. | 86° |
| A. | $\frac{84}{83}$和$\frac{88}{87}$ | B. | $\frac{86}{85}$和$\frac{88}{87}$ | C. | $\frac{85}{84}$和$\frac{87}{86}$ | D. | $\frac{86}{85}$和$\frac{87}{86}$ |
| A. | 42 | B. | -42 | C. | -30 | D. | 30 |
| A. | 3 | B. | 0 | C. | 0或3 | D. | 非上述答案 |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 1 | B. | 3 | C. | $\sqrt{3}$ | D. | 4 |
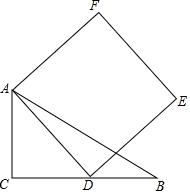 如图.己知△ABC中.∠C=90°,AC=3,BC=4.动点D在边BC上.以AD为边作正方形ADEF.在点D从点C移动至点B的过程中.点E移动的路线长为4$\sqrt{2}$.
如图.己知△ABC中.∠C=90°,AC=3,BC=4.动点D在边BC上.以AD为边作正方形ADEF.在点D从点C移动至点B的过程中.点E移动的路线长为4$\sqrt{2}$.