题目内容
9.某市对城区主干道进行绿化,计划把某一段公路的一侧全部栽上桂花树,要求路的两端各栽一棵,并且每两棵树的间隔相等,如果每隔5米栽1棵,则树苗缺21棵;如果每隔6米栽1棵,则树苗正好用完,设原有树苗x棵,则根据题意列出方程正确的是( )| A. | 5(x+21-1)=6(x-1) | B. | 5(x+21)=6(x-1) | C. | 5(x+21-1)=6x | D. | 5(x+21)=6x |
分析 根据题意可以列出相应的方程,从而可以解答本题.
解答 解:由题意可得,
5(x+21-1)=6(x-1),
故选A.
点评 本题考查由实际问题抽象出一元一次方程,解答本题的关键是明确题意,列出相应的方程,注意要求路的两端各栽一棵.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
20.已知$\frac{b+c-a}{a}$=$\frac{c+a-b}{b}$=$\frac{a+b-c}{c}$,则$\frac{a+b+c}{a-b+c}$的值为( )
| A. | 3 | B. | 0 | C. | 0或3 | D. | 非上述答案 |
17.计算:$\frac{{x}^{2}-x}{x}÷\frac{1-x}{2x}$=( )
| A. | -2x | B. | 2x | C. | -x | D. | x |
4.已知一次函数y=(k-3)x-$\sqrt{3}$,y随x的增大而增大,则下列k的值中可能为( )
| A. | 1 | B. | 3 | C. | $\sqrt{3}$ | D. | 4 |
14.下列四个生活、生产现象:
①用四个钉子就可以把木条固定在墙上;
②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;
③从A地到B地架设电线,总是尽可能沿着线段AB架设;
④把弯曲的公路改直,就能缩短路程,
其中可用“两点之间,线段最短”来解释的现象有( )
①用四个钉子就可以把木条固定在墙上;
②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;
③从A地到B地架设电线,总是尽可能沿着线段AB架设;
④把弯曲的公路改直,就能缩短路程,
其中可用“两点之间,线段最短”来解释的现象有( )
| A. | ①② | B. | ①③ | C. | ②④ | D. | ③④ |
1.已知∠α=35°12′,则∠α的补角的度数是( )
| A. | 54°88′ | B. | 54°48′ | C. | 144°88′ | D. | 144°48′ |
18.一组数据12,16,5,22,4,则这组数据的中位数是( )
| A. | 5 | B. | 12 | C. | 16 | D. | 22 |
19. 一副三角板如图所示放置,则∠AOB等于( )
一副三角板如图所示放置,则∠AOB等于( )
 一副三角板如图所示放置,则∠AOB等于( )
一副三角板如图所示放置,则∠AOB等于( )| A. | 120° | B. | 90° | C. | 105° | D. | 60° |
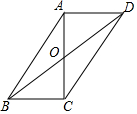 如图,在?ABCD中,对角线AC,BD交于点O,AC⊥BC,若$\frac{BD}{CD}$=$\frac{8}{5}$,则$\frac{BC}{AC}$=$\frac{\sqrt{39}}{6}$.
如图,在?ABCD中,对角线AC,BD交于点O,AC⊥BC,若$\frac{BD}{CD}$=$\frac{8}{5}$,则$\frac{BC}{AC}$=$\frac{\sqrt{39}}{6}$.