题目内容
13.同学们都知道,|4-(-2)|表示4与-2的差的绝对值,实际上也可理解为4与-2两数在数轴上所对应的两点之间的距离;同理|x-3|也可理解为x与3两数在数轴上所对应的两点之间的距离.试探索:(1)|4-(-2)|=6;
(2)找出所有符合条件的整数x,使|x-4|+|x+2|=8成立;
(3)由以上探索猜想,对于任何有理数x,|x-3|+|x-6|是否有最小值?如果有,写出最小值;如果没有,说明理由.
分析 (1)可先算出4与-2的差,然后再求出差的绝对值即可;
(2)设-2、4、x在数轴上所对应的点分别为A、B、X,则有|x-4|+|x+2|=BX+AX=8,AB=|4-(-2)|=6.然后分X在点A的左边、X在AB之间、X在点A的右边三种情况讨论,就可解决问题;
(3)设3、6、x在数轴上所对应的点分别为A、B、X,则|x-3|+|x-6|=AX+BX,AB=|6-3|=3.借鉴(2)中的经验可得AX+BX≥AB,即|x-3|+|x-6|≥3,当X在A、B之间时取等号.
解答 解:(1)|4-(-2)|=|4+2|=6,
故答案为6;
(2)设-2、4、x在数轴上所对应的点分别为A、B、X,
则|x-4|+|x+2|=BX+AX=8,AB=|4-(-2)|=6.
①X在点A的左边时,AX+AB+AX=2AX+6=8,
∴AX=1,∴X所对应的数是-2-1=-3;
②当X在点A、B之间时,BX+AX=AB=8,与AB=6矛盾;
③X在点A的右边时,AB+BX+BX=6+2BX=8,
∴BX=1,∴X所对应的数是4+1=5.
综上所述:符合条件的整数x为-3或5;
(3)对于任何有理数x,|x-3|+|x-6|有最小值,最小值为3.
提示:设3、6、x在数轴上所对应的点分别为A、B、X,
则|x-3|+|x-6|=AX+BX,AB=|6-3|=3.
∵AX+BX≥AB,
∴|x-3|+|x-6|≥3,当X在A、B之间时取等号.
点评 本题考查的是绝对值的概念、几何意义、数轴等知识,在解决问题的过程中用到了分类讨论及数形结合的思想,是解决本题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
3.将下列各式分解因式,正确的是( )
| A. | $\frac{1}{9}$-m2=$\frac{1}{9}$(1+m)(1-m) | B. | 2y2-4xy+2x2=2(x-y)2 | ||
| C. | x3+2x2-x-2=(x+2)(x2-1) | D. | y2-6y-7=(x+1)(x-7) |
1.下列说法错误的是( )
| A. | 抛物线y=2x2的图象向左平移2个单位,再向下平移1个单位,则所得抛物线的解析式为y=2x2-8x+7 | |
| B. | 方程-x2+bx+c=0无实数根,则二次函数y=-x2+bx+c的图象一定在x轴下方 | |
| C. | 将长度为1m的木条黄金分割,较短的一段木条长为$\frac{{3-\sqrt{5}}}{2}$m | |
| D. | 两个等腰直角三角形一定相似 |
18.抛物线y=x2-8x+9的顶点坐标为( )
| A. | (4,7) | B. | (-4,7) | C. | (4,-7) | D. | (-4,-7) |
2.某种新产品的进价是120元,在试销阶段发现产品的日销售量y(件)与每件售价x(元)存在一次函数关系,部分对应值如下表:
(1)请你根据表中所给数据直接写出日销售量y(件)与每件售价x(元)之间的关系式:y=-x+200,自变量x的取值范围是x≥120
(2)在不改变上述关系的情况下,请你帮助商场经理策划每件商品定价为多少元时,每日盈利可达到1600元.
| 日销售量y(件) | 70 | 50 | 35 |
| 每件售价x(元) | 130 | 150 | 165 |
(2)在不改变上述关系的情况下,请你帮助商场经理策划每件商品定价为多少元时,每日盈利可达到1600元.
 若有理数在数轴上的位置如图所示,则化简:|a+c|+|a-b|-|c+a|=a-b.
若有理数在数轴上的位置如图所示,则化简:|a+c|+|a-b|-|c+a|=a-b. 如图是一名考古学家发现的一块古代车轮碎片,你能帮他找到这个车轮的半径吗?(画出示意图,保留作图痕迹)
如图是一名考古学家发现的一块古代车轮碎片,你能帮他找到这个车轮的半径吗?(画出示意图,保留作图痕迹)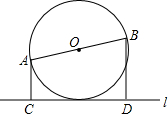 已知,如图所示,AB是⊙O的直径,AC⊥l,BD⊥l,C、D是垂足,且AC+BD=AB,求证:DC是⊙O的切线.
已知,如图所示,AB是⊙O的直径,AC⊥l,BD⊥l,C、D是垂足,且AC+BD=AB,求证:DC是⊙O的切线.