Question

3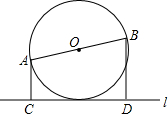．已知，如图所示，AB是⊙O的直径，AC⊥l，BD⊥l，C、D是垂足，且AC+BD=AB，求证：DC是⊙O的切线．

Answer 1

分析 作OE⊥l，根据AC⊥l，BD⊥l，得出AC∥OE∥BD，OA=OB，得出OE是梯形ABDC的中位线，所以OE=$\frac{1}{2}$（AC+BD），由AC+BD=AB得出OE=$\frac{1}{2}$AB，即可证得结论．

解答 证明：作OE⊥l，
∵AC⊥l，BD⊥l，
∴AC∥OE∥BD，
∵OA=OB，
∴CE=DE，
∴OE=$\frac{1}{2}$（AC+BD），
∵AC+BD=AB，
∴OE=$\frac{1}{2}$AB，
∴DC是⊙O的切线．

点评 本题考查了切线的判定，本题的关键是作出辅助线，证得OE是圆的半径．