题目内容
5.等腰三角形ABC的周长为30,其中一个内角的余弦值为$\frac{2}{3}$,则其腰长为9或18-3$\sqrt{6}$.分析 ①若底角余弦值为$\frac{2}{3}$,设其腰长为x,作AD⊥BC,可得BD=15-x,根据余弦函数定义列方程求得x的值即可;②若顶角余弦值为$\frac{2}{3}$,设AC=3x,求得BD=x、CD=$\sqrt{5}$x、BC=$\sqrt{6}$x,利用三角形的周长求得x的值,即可得出答案.
解答 解:①若底角余弦值为$\frac{2}{3}$,如图1,作AD⊥BC于点D,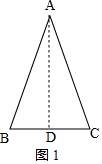
设AB=AC=x,
则BD=CD=$\frac{1}{2}$BC=$\frac{30-2x}{2}$=15-x,
∵cosB=$\frac{BD}{AB}$=$\frac{2}{3}$,
∴$\frac{15-x}{x}$=$\frac{2}{3}$,
解得:x=9,
即腰长为9;
②若顶角余弦值为$\frac{2}{3}$,如图2,作CD⊥AB于点D,
由cosA=$\frac{AD}{AC}$=$\frac{2}{3}$,设AC=3x,则AD=2x,
∴BD=AB-AD=AC-AD=x,CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{(3x)^{2}-(2x)^{2}}$=$\sqrt{5}$x,
∴BC=$\sqrt{B{D}^{2}+C{D}^{2}}$=$\sqrt{{x}^{2}+(\sqrt{5}x)^{2}}$=$\sqrt{6}$x,
由AB+AC+BC=30可得3x+3x+$\sqrt{6}$x=30,
解得:x=6-$\sqrt{6}$,
则腰长为3x=18-3$\sqrt{6}$,
故答案为:9或18-3$\sqrt{6}$.
点评 本题主要考查等腰三角形和解直角三角形,熟练掌握等腰三角形的性质、三角函数的定义及勾股定理是解题的关键.

练习册系列答案
相关题目
 如图,Rt△ABC≌Rt△DCB,两斜边交于点O,如果AC=3,那么OD的长为1.5.
如图,Rt△ABC≌Rt△DCB,两斜边交于点O,如果AC=3,那么OD的长为1.5.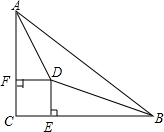 如图,在Rt△ABC中,∠C=90°,∠CAB,∠ABC的平分线交于点D,DE⊥BC于E,DF⊥AC于F,请判断四边形CEDF的形状并说明理由.
如图,在Rt△ABC中,∠C=90°,∠CAB,∠ABC的平分线交于点D,DE⊥BC于E,DF⊥AC于F,请判断四边形CEDF的形状并说明理由. 台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向AB由点A行驶向点B,已知点C为一海港,且点 C与直线 AB上两点A,B的距离分别为300km和400km,又AB=500km,以台风中心为圆心周围250km以内为受影响区域.
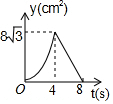
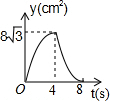
台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向AB由点A行驶向点B,已知点C为一海港,且点 C与直线 AB上两点A,B的距离分别为300km和400km,又AB=500km,以台风中心为圆心周围250km以内为受影响区域. 如图,等边△ABC中,AB=8cm,动点P以2cm/s的速度从点A开始,沿边AC、CB的方向匀速运动至点B停止,PQ⊥AB于点Q,则运动过程中△APQ的面积y(cm2)关于点P的运动时间x(s)的函数图象大致是( )
如图,等边△ABC中,AB=8cm,动点P以2cm/s的速度从点A开始,沿边AC、CB的方向匀速运动至点B停止,PQ⊥AB于点Q,则运动过程中△APQ的面积y(cm2)关于点P的运动时间x(s)的函数图象大致是( )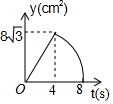
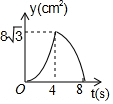
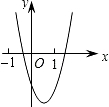 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+a与反比例函数y=$\frac{a+b+c}{x}$在同一坐标内的图象大致为( )
二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+a与反比例函数y=$\frac{a+b+c}{x}$在同一坐标内的图象大致为( )
 已知二次函数y=-$\frac{1}{2}$x2+bx+c的图象与x轴的正半轴相交于点A(2,0)和点B、与y轴相交于点C,它的顶点为M、对称轴与x轴相交于点N.
已知二次函数y=-$\frac{1}{2}$x2+bx+c的图象与x轴的正半轴相交于点A(2,0)和点B、与y轴相交于点C,它的顶点为M、对称轴与x轴相交于点N. 如图,在平面直角坐标系中,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是x>2.
如图,在平面直角坐标系中,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是x>2.