题目内容
5．
如图所示，在平行四边形ABCD中，AC与BD相交于点O，E为OD的中点，连接AE并延长交DC于点F，则DF：FC=（ ）| A． | 1：3 | B． | 1：4 | C． | 2：3 | D． | 1：2 |
分析 首先证明△DFE∽△BAE，然后利用对应边成比例，E为OD的中点，求出DF：AB的值，又知AB=DC，即可得出DF：FC的值．
解答 解：在平行四边形ABCD中，AB∥DC，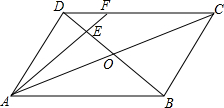
则△DFE∽△BAE，
∴$\frac{DF}{AB}=\frac{DE}{EB}$，
∵O为对角线的交点，
∴DO=BO，
又∵E为OD的中点，
∴DE=$\frac{1}{4}$DB，
则DE：EB=1：3，
∴DF：AB=1：3，
∵DC=AB，
∴DF：DC=1：3，
∴DF：FC=1：2．
故选D．
点评 本题考查了相似三角形的判定与性质以及平行四边形的性质，难度适中，解答本题的关键是根据平行证明△DFE∽△BAE，然后根据对应边成比例求值．
练习册系列答案
相关题目
13．
如图，边长为（m+3）的正方形纸片剪出一个边长为m的正方形之后，剩余部分又剪拼成一个长方形（不重叠无缝隙），若拼成的长方形一边长为3，则周长是（ ）
如图，边长为（m+3）的正方形纸片剪出一个边长为m的正方形之后，剩余部分又剪拼成一个长方形（不重叠无缝隙），若拼成的长方形一边长为3，则周长是（ ）| A． | 2m+6 | B． | 4m+12 | C． | 2m+3 | D． | m+6 |
如图是一数值转换机，若输出的结果为-50，则输入的x的值为±5．
14．如果x=y，a为有理数，那么下列等式不一定成立的是（ ）
| A． | 1-y=1-x | B． | x2=y2 | C． | $\frac{x}{a}$=$\frac{y}{a}$ | D． | ax=ay |
15．方程x2=2x的解是（ ）
| A． | x=2 | B． | x=0 | C． | x1=2，x2=0 | D． | x1=$\sqrt{2}$，x2=0 |