题目内容
如果关于x的方程x3-5x2+(4+k)x-k=0的三个根可以作为一个等腰三角形的三边长,则实数k的值为( )
| A、3 | B、4 | C、5 | D、6 |
考点:高次方程
专题:
分析:根据原方程可知x-1=0,和x2-4x+k=0,因为关于x的方程(x-1)(x2-4x+k)=0有三个根可以作为一个等腰三角形的三边长,所以x2-4x+k=0的根的判别式△=0,然后再由等腰三角形的三边关系来确定k的值.
解答:解:∵关于x的方程x3-5x2+(4+k)x-k=0有三个根,
∵x3-5x2+(4+k)x-k=0
∴(x-1)(x2-4x+k)=0
∴①x-1=0,解得x1=1;
②x2-4x+k=0,
∴△=16-4k=0,即k=4,
∴k的值是k=4.
故选:B.
∵x3-5x2+(4+k)x-k=0
∴(x-1)(x2-4x+k)=0
∴①x-1=0,解得x1=1;
②x2-4x+k=0,
∴△=16-4k=0,即k=4,
∴k的值是k=4.
故选:B.
点评:本题主要考查了根与系数的关系、根的判别式及等腰三角形的三边关系.解答此题时,需注意三个根可以作为一个等腰三角形的三边长.

练习册系列答案
相关题目
有n个人报名参加甲、乙、丙、丁四项体育比赛活动,规定每人至少参加1 项比赛,至多参加2项比赛,但乙、丙两项比赛不能同时兼报,若在所有的报名方式中,必存在一种方式至少有20个人报名,则n的最小值等于( )
| A、171 | B、172 |
| C、180 | D、181 |
若四个互不相等的正实数a,b,c,d满足(a2012-c2012)(a2012-d2012)=2012,(b2012-c2012)(b2012-d2012)=2012,则(ab)2012-(cd)2012的值为( )
| A、-2012 | B、-2011 |
| C、2012 | D、2011 |
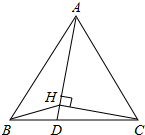 在等边△ABC边BC上取一点D,使BD:DC=1:2,作CH⊥AD于H,连接BH,求证:∠DBH=∠DAB.
在等边△ABC边BC上取一点D,使BD:DC=1:2,作CH⊥AD于H,连接BH,求证:∠DBH=∠DAB. 如图,三角形ABC各边的四等分点D,E,F分别与点C,B,A相连,得到一个小三角形GHI,那么三角形GHI的面积与三角形ABC的面积的比是
如图,三角形ABC各边的四等分点D,E,F分别与点C,B,A相连,得到一个小三角形GHI,那么三角形GHI的面积与三角形ABC的面积的比是


