题目内容
20.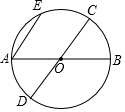 已知:如图,AB,CD是⊙O的直径,AE是⊙O的弦,若AE∥CD,求证:$\widehat{AD}$=$\widehat{BC}$=$\widehat{EC}$.
已知:如图,AB,CD是⊙O的直径,AE是⊙O的弦,若AE∥CD,求证:$\widehat{AD}$=$\widehat{BC}$=$\widehat{EC}$.
分析 先根据AE∥CD可得出$\widehat{AD}$=$\widehat{EC}$,再由∠AOD=∠BOC可得出$\widehat{AD}$=$\widehat{BC}$,进而可得出结论.
解答 证明:∵AE∥CD,
∴$\widehat{AD}$=$\widehat{EC}$.
∵∠AOD=∠BOC,
∴$\widehat{AD}$=$\widehat{BC}$,
∴$\widehat{AD}$=$\widehat{BC}$=$\widehat{EC}$.
点评 本题考查的是圆心角、弧、弦的关系,熟知在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.如图,在数轴上表示互为相反数的两数的点是( )


| A. | 点A和点C | B. | 点B和点A | C. | 点C和点B | D. | 点D和点B |
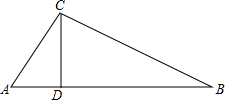 如图,在△ABC中,∠ACB=90°,过点C作CD⊥AB于D,AC=3cm,BC=4cm,AB=5cm.
如图,在△ABC中,∠ACB=90°,过点C作CD⊥AB于D,AC=3cm,BC=4cm,AB=5cm.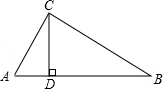 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若∠B=30°,CD=6,求AB的长.
如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若∠B=30°,CD=6,求AB的长.