题目内容
11.△ABC中,AC=6,BC=8,AB=10,D为AB的中点,点E在BC边上,且DE=$\sqrt{13}$,则tan∠AEC=$\frac{1}{3}$或1.分析 由勾股定理逆定理知∠C=90°,作DF⊥BC可得DF∥AC,根据D为AB中点得DB=$\frac{1}{2}$AB=5,BF=CF=$\frac{1}{2}$BC=4,继而可得DF=3,根据勾股定理可得EF=2,分点E在CF上和点E在BF上分别求得CE的长,最后由三角函数定义可得答案.
解答 解:∵AC=6,BC=8,AB=10,
∴AC2+BC2=AB2,
∴∠C=90°,
如图1,过点D作DF⊥BC于点F,
∴DF∥AC,
∵D为AB中点,
∴DB=$\frac{1}{2}$AB=5,BF=CF=$\frac{1}{2}$BC=4,
∴DF=$\sqrt{D{B}^{2}-B{F}^{2}}$=3,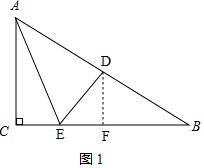
①当点E在CF上时,
∵DE=$\sqrt{13}$,
∴EF=$\sqrt{D{E}^{2}-D{F}^{2}}$=2,
∴CE=CF-EF=2,
∴tan∠AEC=$\frac{CE}{AC}$=$\frac{2}{6}$=$\frac{1}{3}$;
②如图2,当点E在BF上时,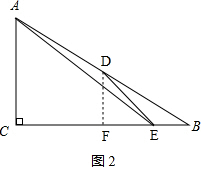
CE=CF+EF=6,
∴tan∠AEC=$\frac{CE}{AC}$=$\frac{6}{6}$=1,
综上,tan∠AEC=$\frac{1}{3}$或1,
故答案为:$\frac{1}{3}$或1.
点评 本题主要考查勾股定理及其逆定理和平行线等分线段定理、三角函数定义,根据DE的长知道存在两种情况是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.如果甲数为x,乙数比甲数多4倍,则乙数为( )
| A. | 4x | B. | 5x | C. | $\frac{1}{4}$x | D. | $\frac{1}{5}$x |
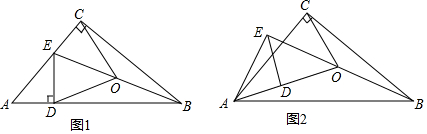

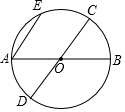 已知:如图,AB,CD是⊙O的直径,AE是⊙O的弦,若AE∥CD,求证:$\widehat{AD}$=$\widehat{BC}$=$\widehat{EC}$.
已知:如图,AB,CD是⊙O的直径,AE是⊙O的弦,若AE∥CD,求证:$\widehat{AD}$=$\widehat{BC}$=$\widehat{EC}$.