题目内容
10.若在△ABC中,a=m2-n2,b=2mn,c=m2+n2,则△ABC是直角三角形.分析 根据题意可得出a、b、c的表达式,然后分别平方可得出c2=a2+b2,从而利用勾股定理的逆定理即可作出证明.
解答 解:∵在△ABC中,a=m2-n2,b=2mn,c=m2+n2,
∴a2=m4-2m2n2+n4,b2=4m2n2,c2=m4+2m2n2+n4,
∴c2=a2+b2,
∴△ABC是直角三角形.
故答案为:直角.
点评 此题考查了勾股定理的逆定理,解答本题的关键是熟练运用勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
18. 点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长( )
点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长( )
 点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长( )
点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长( )| A. | 1 cm | B. | 2 cm | C. | 4 cm | D. | 6 cm |
2.如果甲数为x,乙数比甲数多4倍,则乙数为( )
| A. | 4x | B. | 5x | C. | $\frac{1}{4}$x | D. | $\frac{1}{5}$x |
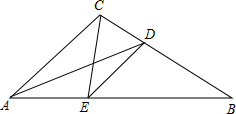 如图,△ABC,∠BAC=40°,AD平分∠BAC,点E是AB上一点,连接CE、DE,∠ACE=40°,∠ADC=50°,求∠CED的度数.
如图,△ABC,∠BAC=40°,AD平分∠BAC,点E是AB上一点,连接CE、DE,∠ACE=40°,∠ADC=50°,求∠CED的度数.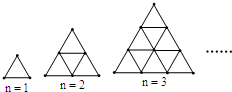 如图,是用火柴棍摆出的一系列三角形图案,按这种方式摆下去,当每边摆上20(n=20)根时,需火柴棍为630 根,若当每边摆上n根时,试写出需火柴棍为$\frac{3n(1+n)}{2}$ 根.
如图,是用火柴棍摆出的一系列三角形图案,按这种方式摆下去,当每边摆上20(n=20)根时,需火柴棍为630 根,若当每边摆上n根时,试写出需火柴棍为$\frac{3n(1+n)}{2}$ 根.
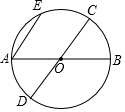 已知:如图,AB,CD是⊙O的直径,AE是⊙O的弦,若AE∥CD,求证:$\widehat{AD}$=$\widehat{BC}$=$\widehat{EC}$.
已知:如图,AB,CD是⊙O的直径,AE是⊙O的弦,若AE∥CD,求证:$\widehat{AD}$=$\widehat{BC}$=$\widehat{EC}$.