题目内容
15.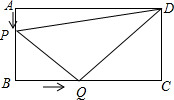 如图所示,在长方形ABCD中,AB=6厘米,BC=12厘米,点P沿AB边从点A开始向点B以1厘米/秒的速度移动,点Q沿BC从点B开始向点C以2厘米/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6).
如图所示,在长方形ABCD中,AB=6厘米,BC=12厘米,点P沿AB边从点A开始向点B以1厘米/秒的速度移动,点Q沿BC从点B开始向点C以2厘米/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6).(1)PB=2厘米时,求点P移动多少秒?
(2)t为何值时,△PBQ为等腰直角三角形?
(3)求四边形PBQD的面积.
分析 (1)由AB、PB的长可求得AP的长,则可求得t的值;
(2)根据等腰直角三角形的性质可求得PB=BQ,则可得到关于t的方程,可求得t的值;
(3)可用t分别表示出S△APD、S△QCD,再利用面积的和差可求得四边形PBQD的面积.
解答 解:
(1)∵PB=2cm,AB=6cm,
∴AP=AB-PB=6-2=4(秒),
即点P移动4秒;
(2)∵△PBQ为等腰直角三角形,
∴PB=BQ,即6-t=2t,解得t=2
∴当t的值为2秒时,△PBQ为等腰直角三角形;
(3)由题意可知AP=t,AB=6,BQ=2t,BC=12,
∴PB=6-t,QC=12-2t,CD=6,AD=12,
∴S△APD=$\frac{1}{2}$AP•AD=$\frac{1}{2}$t×12=6t,S△QCD=$\frac{1}{2}$QC•CD=$\frac{1}{2}$(12-2t)6=36-6t,
∴S四边形PBQD=S矩形ABCD-S△APD-S△QCD=72-6t-(36-6t)=36cm2,
点评 本题为四边形的综合应用,涉及等腰三角形的性质、三角形的面积、方程的思想及转化思想.用t表示出相应线段的长度,化动为静是解决这类运动型问题的一般思想.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 如图,在?ABCD中,EF过角线的交点O,若AD=8cm,AB=6cm,OE=4cm,求四边形ABFE的周长.
如图,在?ABCD中,EF过角线的交点O,若AD=8cm,AB=6cm,OE=4cm,求四边形ABFE的周长. 如图,BE平分∠ABF,DF⊥AB交AB于点D,AC⊥BF交BF于点C,AC,FD相交于点E,若∠F=30°,DE=1,求AC的长.
如图,BE平分∠ABF,DF⊥AB交AB于点D,AC⊥BF交BF于点C,AC,FD相交于点E,若∠F=30°,DE=1,求AC的长.
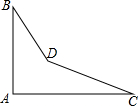 如图,是一个零件的形状,按规定∠A应等于90°,∠B与∠C分别是32°和27°,检测工人量得∠BDC=150°,问该零件是否合格?为什么?
如图,是一个零件的形状,按规定∠A应等于90°,∠B与∠C分别是32°和27°,检测工人量得∠BDC=150°,问该零件是否合格?为什么?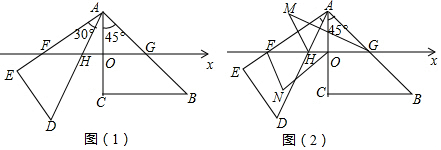
 如图,在平面直角坐标系中,A(2,2),B(-1,0),C (3,0)
如图,在平面直角坐标系中,A(2,2),B(-1,0),C (3,0)