题目内容
4.矩形ABCD的边AB、BC的长分别是关于x的方程x2+(2m-1)x+m2+3=0的根.(1)若矩形ABCD是正方形,求m的值.
(2)若矩形ABCD的面积为12时,求m的值.
分析 (1)首先根据正方形的两边相等得到方程的两根相等,从而利用根的判别式确定m的值;
(2)由矩形的面积得出方程,解方程即可.
解答 解:(1)∵四边形ABCD是正方形,
∴AB=AD,
又∵△=(2m-1)2-4×1×(m2+3)=0,
解得:m=-$\frac{11}{4}$;
即m=-$\frac{11}{4}$时,四边形ABCD是正方形;
(2)根据题意得:AB•BC=m2+3=12,
解得:m=±3(正值舍去),
∴m=-3.
点评 本题考查了正方形的性质、矩形的性质、一元二次方程的应用及根的判别式的知识,解题的关键是结合正方形的性质得到方程有两根相等的实数根,从而确定方程的解,难道不大.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
16.小明的哥哥是一名大学生,他利用暑假去一家公司打工,报酬按20元/小时计算,设小明得哥哥这个月的工作时间为t(小时),应得报酬为m(元),请填写下表,然后回答下面问题
(1)你能用含t的代数式表示m的值吗?
(2)在上述问题中,那些是常量?那么是变量?
| 工作时间t(小时) | 1 | 5 | 10 | 15 | 20 | … | t | … |
| 报酬m(元) | 20 | 100 | 200 | 300 | 400 | … | 20t | … |
(2)在上述问题中,那些是常量?那么是变量?
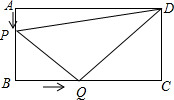 如图所示,在长方形ABCD中,AB=6厘米,BC=12厘米,点P沿AB边从点A开始向点B以1厘米/秒的速度移动,点Q沿BC从点B开始向点C以2厘米/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6).
如图所示,在长方形ABCD中,AB=6厘米,BC=12厘米,点P沿AB边从点A开始向点B以1厘米/秒的速度移动,点Q沿BC从点B开始向点C以2厘米/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6).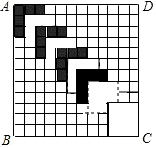 如图,正方形ABCD的边长为12,划分成12×12个小正方形格.将边长为n(n为整数,且2≤n≤11)的黑白两色正方形纸片按图中的方式黑白相间地摆放,第一张n×n的纸片正好盖住正方形ABCD左上角的n×n个小正方形格,第二张纸片盖住第一张纸片的部分恰好为(n-1)×(n-1)的正方形.如此摆放下去,最后直到纸片盖住正方形ABCD的右下角为止.请你认真观察思考后回答下列问题:
如图,正方形ABCD的边长为12,划分成12×12个小正方形格.将边长为n(n为整数,且2≤n≤11)的黑白两色正方形纸片按图中的方式黑白相间地摆放,第一张n×n的纸片正好盖住正方形ABCD左上角的n×n个小正方形格,第二张纸片盖住第一张纸片的部分恰好为(n-1)×(n-1)的正方形.如此摆放下去,最后直到纸片盖住正方形ABCD的右下角为止.请你认真观察思考后回答下列问题: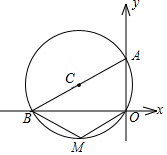 如图,⊙C过原点,且与两坐标轴分别交于点A,点B,点A的坐标为(0,3),M是第三象限内弧上一点,∠BMO=120°,求⊙C的半径长.
如图,⊙C过原点,且与两坐标轴分别交于点A,点B,点A的坐标为(0,3),M是第三象限内弧上一点,∠BMO=120°,求⊙C的半径长.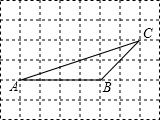 如图,在方格纸中,点A、B、C是三个格点(网格线的交点叫做格点)
如图,在方格纸中,点A、B、C是三个格点(网格线的交点叫做格点)