题目内容
6.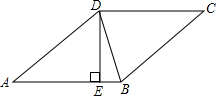 如图所示,菱形ABCD的周长为20 cm,DE⊥AB,垂足为E,sinA=$\frac{3}{5}$,则下列结论错误的是( )
如图所示,菱形ABCD的周长为20 cm,DE⊥AB,垂足为E,sinA=$\frac{3}{5}$,则下列结论错误的是( )| A. | DE=3 cm | B. | BE=1 cm | ||
| C. | 菱形的面积为15 cm2 | D. | BD=2$\sqrt{10}{cm}$ |
分析 由菱形ABCD的周长为20 cm,推出AD=AB=5,由DE⊥AB,推出∠AED=90°,在Rt△ADE中,sin∠A=$\frac{3}{5}$=$\frac{DE}{AD}$,推出DE=3,AE=$\sqrt{A{D}^{2}-D{E}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,推出EB=AB-AE=1,推出BD=$\sqrt{D{E}^{2}+E{B}^{2}}$=$\sqrt{10}$,推出菱形ABCD的面积=AB•DE=15.由此即可判断.
解答 解: ∵菱形ABCD的周长为20 cm,
∵菱形ABCD的周长为20 cm,
∴AD=AB=5,
∵DE⊥AB,
∴∠AED=90°,
在Rt△ADE中,sin∠A=$\frac{3}{5}$=$\frac{DE}{AD}$,
∴DE=3,AE=$\sqrt{A{D}^{2}-D{E}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴EB=AB-AE=1,
∴BD=$\sqrt{D{E}^{2}+E{B}^{2}}$=$\sqrt{10}$,
∴菱形ABCD的面积=AB•DE=15.
故选D.
点评 本题考查菱形的判定、解直角三角形、勾股定理锐角三角函数等知识,解题的关键是灵活运用所学知识,属于基础题,中考常考题型.

练习册系列答案
相关题目
15.已知一个反比例函数的图象经过点A(3,-4),那么不在这个函数图象上的点是( )
| A. | (-3,-4) | B. | (-3,4) | C. | (2,-6) | D. | ($\frac{\sqrt{2}}{2}$,-12$\sqrt{2}$) |
1. 如图,从直径为4cm的圆形纸片中,剪出一个圆心角为90°的扇OAB,且点O、A、B在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是( )
如图,从直径为4cm的圆形纸片中,剪出一个圆心角为90°的扇OAB,且点O、A、B在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是( )
 如图,从直径为4cm的圆形纸片中,剪出一个圆心角为90°的扇OAB,且点O、A、B在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是( )
如图,从直径为4cm的圆形纸片中,剪出一个圆心角为90°的扇OAB,且点O、A、B在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是( )| A. | $\frac{\sqrt{2}}{2}$ cm | B. | $\sqrt{2}$cm | C. | 1 cm | D. | 2 cm |
11.在函数y=$\frac{{\sqrt{x-3}}}{x-3}$中,自变量x的取值范围是( )
| A. | x>3 | B. | x≥3 | C. | x≠-3 | D. | x>-3且x≠0 |
16.下列运算正确的是( )
| A. | 2a+3b=5ab | B. | x2+x4=x6 | C. | x6÷x3=x2 | D. | (-x3)2=x6 |

 如图,下面的几何体由两个大小相同的正方体和一个圆柱体组成,则它的左视图是( )
如图,下面的几何体由两个大小相同的正方体和一个圆柱体组成,则它的左视图是( )


