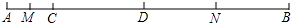题目内容
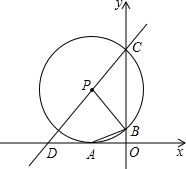 如图,点P坐标为(-3,5),以P为圆心的⊙P与x轴相切于点A,与y轴交于B、C两点,连接PB、AB.
如图,点P坐标为(-3,5),以P为圆心的⊙P与x轴相切于点A,与y轴交于B、C两点,连接PB、AB.(1)求证:AB平分∠PBO;
(2)若直线CP交x轴于点D,求出点D的坐标.
考点:圆的综合题
专题:
分析:(1)连接AP,根据切线的性质定理以及圆的半径处处相等所形成的等腰三角形PAB的性质即可证明AB平分∠PBO;
(2)过P作PH⊥BC于H,根据P的坐标易求圆的半径为5,利用勾股定理可求出BH=4,所以OB=1,由垂径定理可得OC=9,易证△DAP∽△DOC,由相似三角形OD的性质:对应边的比值相等即可求出DA的长,进而可求出OD的长,所以D的坐标即可求出.
(2)过P作PH⊥BC于H,根据P的坐标易求圆的半径为5,利用勾股定理可求出BH=4,所以OB=1,由垂径定理可得OC=9,易证△DAP∽△DOC,由相似三角形OD的性质:对应边的比值相等即可求出DA的长,进而可求出OD的长,所以D的坐标即可求出.
解答: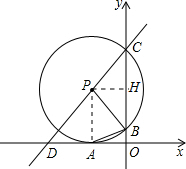 (1)证明:连接AP,
(1)证明:连接AP,
∵⊙P与x轴相切于点A,
∴∠PA0=90°,
∴∠PAB+∠BAO=90°,
∵∠DOC=90°,
∴∠BAO+∠ABO=90°,
∵PB=PA,
∴∠PAB=∠PBA,
∴∠PBA=∠ABO,
∴AB平分∠PBO;
(2)过P作PH⊥BC于H,
∴BH=CH,
∵点P坐标为(-3,5),
∴PA=PB=5,PH=AO=3,
∴BH=
=4,
∴OB=1,
∴CO=9,
∵PA∥OC,
∴△DAP∽△DOC,
∴
=
,
∴
=
,
解得:DA=
,
∴DO=DA+AO=3+
=
,
∴点D的坐标为(-
,0).
 (1)证明:连接AP,
(1)证明:连接AP,∵⊙P与x轴相切于点A,
∴∠PA0=90°,
∴∠PAB+∠BAO=90°,
∵∠DOC=90°,
∴∠BAO+∠ABO=90°,
∵PB=PA,
∴∠PAB=∠PBA,
∴∠PBA=∠ABO,
∴AB平分∠PBO;
(2)过P作PH⊥BC于H,
∴BH=CH,
∵点P坐标为(-3,5),
∴PA=PB=5,PH=AO=3,
∴BH=
| PB2-PH2 |
∴OB=1,
∴CO=9,
∵PA∥OC,
∴△DAP∽△DOC,
∴
| PA |
| OC |
| DA |
| DO |
∴
| 5 |
| 9 |
| DA |
| DA+3 |
解得:DA=
| 15 |
| 4 |
∴DO=DA+AO=3+
| 15 |
| 4 |
| 27 |
| 4 |
∴点D的坐标为(-
| 27 |
| 4 |
点评:本题考查了切线的性质定理、圆的半径处处相等的性质、垂径定理的运用、勾股定理的运用以及相似三角形的判定和性质,题目的综合性较强,难度中等,解题的关键是正确作出辅助线构造直角三角形.

练习册系列答案
相关题目
 (1)如图1、图2,点P是⊙O外一点,作直线OP,交⊙O于点M、N,则有结论:①点M是点P到⊙O的最近点;②点N是点P到⊙O的最远点.
(1)如图1、图2,点P是⊙O外一点,作直线OP,交⊙O于点M、N,则有结论:①点M是点P到⊙O的最近点;②点N是点P到⊙O的最远点.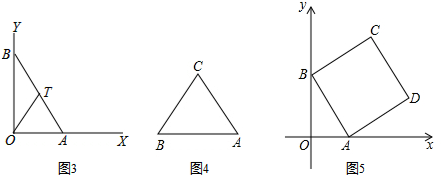
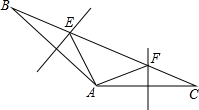 如图,在△ABC中,边AB、AC的垂直平分线分别交BC于E、F.
如图,在△ABC中,边AB、AC的垂直平分线分别交BC于E、F.