题目内容
在四边形ABCD中,AB=5,BC=3,DE⊥AC于E,DE=3,S△DAC=6,求∠ACB.
考点:勾股定理的逆定理
专题:
分析:先根据三角形的面积求出AC长,求出AC2+BC2=AB2,根据勾股定理的逆定理求出即可.
解答:
解:∵DE⊥AC,DE=3,S△DAC=6,
∴
×AC×DE=6,
∴AC=4,
∵AB=5,BC=3,
∴AC2+BC2=AB2,
∴∠ACB=90°.

解:∵DE⊥AC,DE=3,S△DAC=6,
∴
| 1 |
| 2 |
∴AC=4,
∵AB=5,BC=3,
∴AC2+BC2=AB2,
∴∠ACB=90°.
点评:本题考查了勾股定理的逆定理和三角形的面积的应用,注意:在一个三角形中,如果有两边的平方和等于第三边的平方,那么这个三角形是直角三角形.

练习册系列答案
相关题目
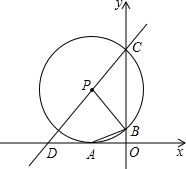 如图,点P坐标为(-3,5),以P为圆心的⊙P与x轴相切于点A,与y轴交于B、C两点,连接PB、AB.
如图,点P坐标为(-3,5),以P为圆心的⊙P与x轴相切于点A,与y轴交于B、C两点,连接PB、AB.