题目内容
6.若关于x的一元二次方程为ax2+bx+c=0的两根之和为3,则关于x的方程a(x+1)2+b(x+1)+c=0的两根之和为1.分析 设方程ax2+bx+c=0的两根分别为x1,x2,则方程a(x+1)2+b(x+1)+c=0的两根分别为x1-1,x2-1,根据根与系数的关系可得x1+x2=3,进而即可得出(x1-1)+(x2-1)的值,此题得解.
解答 解:设方程ax2+bx+c=0的两根分别为x1,x2,则方程a(x+1)2+b(x+1)+c=0的两根分别为x1-1,x2-1,
由题意得:x1+x2=3,
∴(x1-1)+(x2-1)=(x1+x2)-1-1=1.
故答案为:1.
点评 本题考查了根与系数的关系,根据根与系数的关系找出x1+x2=3是解题的关键.

练习册系列答案
相关题目
14.已知m是方程x2-x+1=0的一个根,则代数式m2-m的值等于( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
15.下列一元二次方程中,没有实数根的方程是( )
| A. | x2-3x+1=0 | B. | x2+2x-1=0 | C. | x2-2x+1=0 | D. | x2+2x+3=0 |
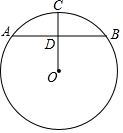 已知,如图,OC是⊙O的半径,AB是弦,OC⊥AB于D,AB=8,OD=CD+1,求⊙O的半径.
已知,如图,OC是⊙O的半径,AB是弦,OC⊥AB于D,AB=8,OD=CD+1,求⊙O的半径.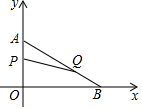 如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.