题目内容
若关于x的方程2x2-3x+m=0的一个根大于-2且小于-1,另一个根大于2且小于3,则m的取值范围是( )
A、m<
| ||
B、-14<m<
| ||
| C、-9<m<-5 | ||
| D、-14<m<-2 |
考点:一元二次方程根的分布
专题:计算题
分析:先求出判别式大于零下m的范围,然后根据二次函数的性质及根的分布可得出f(-2)>0且f(-1)<0;及f(2)<0且f(3)>0,分别解出联立即可得出m的范围.
解答:解:由题意得,f(x)=2x2-3x+m为开口向上的一元二次函数,如图所示:

由已知可知,方程有两不等的实根,则△=(-3)2-4×2×m=9-8m>0,即m<
;
又因为f(x)开口向上,根据此一元二次的函数的图象及性质,
方程的一根-2<x1<-1,则有:f(-2)>0,即8+6+m>0;且f(-1)<0,即2+3+m<0;
方程的另一根为2<x2<3,则有:f(2)<0,即8-6+m<0;且f(3)>0,即18-9+m>0;
由以上四个不等式联立求解(取交集)得:-9<m<-5,
此时,使得△>0,m<
成立.
故选C.

由已知可知,方程有两不等的实根,则△=(-3)2-4×2×m=9-8m>0,即m<
| 9 |
| 8 |
又因为f(x)开口向上,根据此一元二次的函数的图象及性质,
方程的一根-2<x1<-1,则有:f(-2)>0,即8+6+m>0;且f(-1)<0,即2+3+m<0;
方程的另一根为2<x2<3,则有:f(2)<0,即8-6+m<0;且f(3)>0,即18-9+m>0;
由以上四个不等式联立求解(取交集)得:-9<m<-5,
此时,使得△>0,m<
| 9 |
| 8 |
故选C.
点评:此题考查了一元二次方程根的分布,根据根的分布范围得出函数上一些点的函数值的范围是解答本题的关键,有一定难度.

练习册系列答案
相关题目
若不论k取什么实数,关于x的方程
-
=1(a、b是常数)的根总是x=1,则a+b=( )
| 2kx+a |
| 3 |
| x-bk |
| 6 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
已知函数y=(a-2)x-3a-1,当自变量x的取值范围是3≤x≤5时,y既能达到大于5的值,又能取到小于3的值,则实数a的取值范围是( )
| A、a<3 | B、a>5 |
| C、a>8 | D、任意实数 |
 如图,一张半径为1的圆形纸片在边长为4的正方形内任意移动,则在该正方形内,这张圆形纸片“能接触到的部分”的面积是( )
如图,一张半径为1的圆形纸片在边长为4的正方形内任意移动,则在该正方形内,这张圆形纸片“能接触到的部分”的面积是( )| A、4-π | ||
| B、π | ||
| C、12+π | ||
D、15+
|
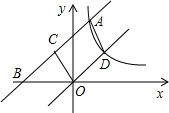 如图,直线y=x+3交反比例函数
如图,直线y=x+3交反比例函数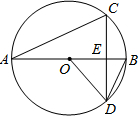 如图,AB为⊙O的直径,弦CD⊥AB于E,∠CDB=15°,OE=2
如图,AB为⊙O的直径,弦CD⊥AB于E,∠CDB=15°,OE=2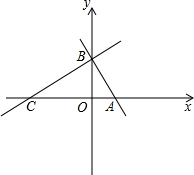 如图,在平面直角坐标系中,点C(-3,0),点A、B分别在x轴、y轴的正半轴上,且满足(OB-
如图,在平面直角坐标系中,点C(-3,0),点A、B分别在x轴、y轴的正半轴上,且满足(OB-