题目内容
等腰梯形ABCD中,AD∥BC,对角线AC与BD相交于P,已知∠APD=60°,AD=2,BC=4,则梯形ABCD的面积为 .
考点:等腰梯形的性质
专题:
分析:过点D作DE⊥BC,求出∠BPC=60°,再证出△ABC≌△DCB得出∠DBC=∠ACB=60°,然后根据AD=2,BC=4,求出BE,从而根据DE=tan60°•BE得出DE的长,最后代入梯形ABCD的面积为
(AD+BC)•DE即可得出答案.
| 1 |
| 2 |
解答: 解:过点D作DE⊥BC,
解:过点D作DE⊥BC,
∵∠APD=60°,
∴∠BPC=60°,
在△ABC和△DCB中
∴△ABC≌△DCB
∴∠DBC=∠ACB=60°,
∵AD=2,BC=4,
∴CE=(4-2)÷2=1,
∴BE=4-1=3,
∴DE=tan60°•BE=
×3=3
,
∴梯形ABCD的面积为
(AD+BC)•DE=
×(2+4)×3
=9
.
故答案为:9
.
 解:过点D作DE⊥BC,
解:过点D作DE⊥BC,∵∠APD=60°,
∴∠BPC=60°,
在△ABC和△DCB中
|
∴△ABC≌△DCB
∴∠DBC=∠ACB=60°,
∵AD=2,BC=4,
∴CE=(4-2)÷2=1,
∴BE=4-1=3,
∴DE=tan60°•BE=
| 3 |
| 3 |
∴梯形ABCD的面积为
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
故答案为:9
| 3 |
点评:此题考查了等腰梯形的性质;用到的知识点是等腰梯形的性质、全等三角形的性质与判定、解直角三角形等,关键是根据已知条件作出辅助线,求出线段的长.

练习册系列答案
相关题目
一辆标致307以30m/s的速度在汉宜高速公路上疾驰,司机突然发现前方路面有情况,紧急刹车后小车滑行了75m后停止,给出如下判断:①从刹车到停车用了5秒;②从刹车到停车平均每秒车速减少值为6m/s;③刹车后汽车滑行到48m时约用了2s钟.
其中判断正确的是( )
其中判断正确的是( )
| A、①② | B、②③ | C、①③ | D、①②③ |
 如图,已知△ABC中,∠B=90°,AB=3,BC=
如图,已知△ABC中,∠B=90°,AB=3,BC=| 3 |
| 6 |
| A、10° | B、15° |
| C、20° | D、25° |
两圆的直径分别为4和6,圆心距为10,则两圆的位置关系为( )
| A、外离 | B、外切 | C、相交 | D、内切 |
若关于x的方程2x2-3x+m=0的一个根大于-2且小于-1,另一个根大于2且小于3,则m的取值范围是( )
A、m<
| ||
B、-14<m<
| ||
| C、-9<m<-5 | ||
| D、-14<m<-2 |
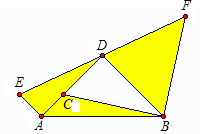 如图,等腰直角三角形ABD,点C是直角边AD上的动点,连接CB.现在将点C绕点A逆时针方向旋转90°得点E,再将点C绕点B顺时针方向旋转90°得点F.如果AD=BD=
如图,等腰直角三角形ABD,点C是直角边AD上的动点,连接CB.现在将点C绕点A逆时针方向旋转90°得点E,再将点C绕点B顺时针方向旋转90°得点F.如果AD=BD= 如图,正方形OA1B1C1,C1A2B2C2,C2A3B3C3,…的顶点A1,A2,A3,…在直线y=kx+b上,顶点C1,C2,C3,…在x轴上,已知B1(1,1),B2(3,2),那么点A4的坐标为
如图,正方形OA1B1C1,C1A2B2C2,C2A3B3C3,…的顶点A1,A2,A3,…在直线y=kx+b上,顶点C1,C2,C3,…在x轴上,已知B1(1,1),B2(3,2),那么点A4的坐标为 如图,两个同心圆,大圆的弦AB切小圆于点C,且AB=10,则图中阴影部分面积为
如图,两个同心圆,大圆的弦AB切小圆于点C,且AB=10,则图中阴影部分面积为