题目内容
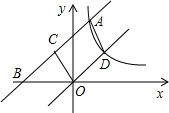 如图,直线y=x+3交反比例函数y=
如图,直线y=x+3交反比例函数y=| k |
| x |
| k |
| x |
考点:反比例函数综合题
专题:压轴题
分析:首先根据A在直线y=x+3上,设点A(a,a+3),求出B点坐标,再由条件线段OD所在直线是由直线y=x+3平移得到的,可得线段OD的直线为y=x,且CA=DO,设点D(d,d),再根据勾股定理表示出线段AC、OD的长:CA2=(a+1)2+(a+1)2,OD2=d2+d2,再由CA=DO可得(a+1)2=d2,再根据点A、点D都在反比例函数y=
上,可得(a+3)a=k、d2=k,把两式结合即可求出k、a的值.
| k |
| x |
解答:解:根据题意画出图:
∵A在直线y=x+3上,
∴设点A(a,a+3);
∵直线y=x+3交x轴于点B,
∴B(-3,0),
∵线段OD所在直线是由直线y=x+3平移得到的,
∴线段OD的直线为y=x,设点D(d,d),
∵线段CA平移到OD,
∴|CA|=|OD|;
∵A(a,a+3)、B(-3,0)、C(-1,2)、D(d,d),
∴CA2=(a+1)2+(a+1)2,OD2=d2+d2,
解之得(a+1)2=d2…①
又∵点A、点D都在反比例函数y=
上,
∴(a+3)a=k、d2=k…②
∴(a+3)a=d2,
∴(a+3)a=(a+1)2,
解得:a=1,k=4.
故答案为:4.
∵A在直线y=x+3上,
∴设点A(a,a+3);
∵直线y=x+3交x轴于点B,
∴B(-3,0),
∵线段OD所在直线是由直线y=x+3平移得到的,
∴线段OD的直线为y=x,设点D(d,d),
∵线段CA平移到OD,
∴|CA|=|OD|;
∵A(a,a+3)、B(-3,0)、C(-1,2)、D(d,d),
∴CA2=(a+1)2+(a+1)2,OD2=d2+d2,
解之得(a+1)2=d2…①
又∵点A、点D都在反比例函数y=
| k |
| x |
∴(a+3)a=k、d2=k…②
∴(a+3)a=d2,
∴(a+3)a=(a+1)2,
解得:a=1,k=4.
故答案为:4.
点评:此题主要考查了一次函数、反比例函数、勾股定理,关键是根据题意表示出A、B、C、D的坐标,用勾股定理与函数关系式表示出a、k的关系.

练习册系列答案
相关题目
两圆的直径分别为4和6,圆心距为10,则两圆的位置关系为( )
| A、外离 | B、外切 | C、相交 | D、内切 |
若关于x的方程2x2-3x+m=0的一个根大于-2且小于-1,另一个根大于2且小于3,则m的取值范围是( )
A、m<
| ||
B、-14<m<
| ||
| C、-9<m<-5 | ||
| D、-14<m<-2 |
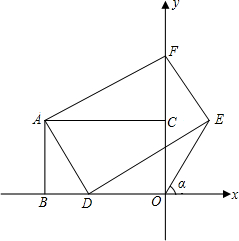 的一个动点,连接AD,过A作AD的垂线交y轴于F点,并以AF、AD为边作矩形ADEF.
的一个动点,连接AD,过A作AD的垂线交y轴于F点,并以AF、AD为边作矩形ADEF. 如图,正方形OA1B1C1,C1A2B2C2,C2A3B3C3,…的顶点A1,A2,A3,…在直线y=kx+b上,顶点C1,C2,C3,…在x轴上,已知B1(1,1),B2(3,2),那么点A4的坐标为
如图,正方形OA1B1C1,C1A2B2C2,C2A3B3C3,…的顶点A1,A2,A3,…在直线y=kx+b上,顶点C1,C2,C3,…在x轴上,已知B1(1,1),B2(3,2),那么点A4的坐标为 如图,两个同心圆,大圆的弦AB切小圆于点C,且AB=10,则图中阴影部分面积为
如图,两个同心圆,大圆的弦AB切小圆于点C,且AB=10,则图中阴影部分面积为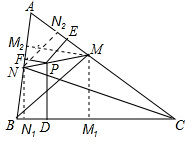 为∠ABC的平分线,MP的延长线交AB于点N.如果PD=PE+PF,求证:CN是∠ACB的平分线.
为∠ABC的平分线,MP的延长线交AB于点N.如果PD=PE+PF,求证:CN是∠ACB的平分线.