题目内容
3.某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误.
回答下列问题:
(1)写出条形图中存在的错误,并说明理由;
(2)写出这20名学生每人植树量的众数、中位数;
(3)求这20名学生每人植树量的平均数,并估计这260名学生共植树多少棵.
分析 (1)利用总人数20乘以对应的百分比即可求得D类的人数解答;
(2)根据众数、中位数的定义即可直接求解;
(3)首先求得调查的20人的平均数,乘以总人数260即可.
解答 解(1)D错误,理由为:20×10%=2≠3(人).
(2)众数为5棵,中位数为5棵
(3)$\overline{x}$=$\frac{4×4+5×8+6×6+7×2}{20}$=5.3(棵).
估计260名学生共植树5.3×260=1378(棵).
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
13.已知二次函数y=ax2-bx+$\frac{1}{2}$b-a与x轴交于A、B两点,则线段AB的最小值为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 无法确定 |
14. 如图是正方体的展开图,原正方体相对两个面上的数字和最大是( )
如图是正方体的展开图,原正方体相对两个面上的数字和最大是( )
 如图是正方体的展开图,原正方体相对两个面上的数字和最大是( )
如图是正方体的展开图,原正方体相对两个面上的数字和最大是( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
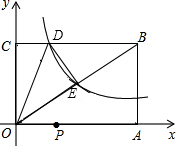 如图,已知矩形OABC的两边OA、OC分别落在x轴、y轴的正半轴上,顶点B的坐标是(6,4),反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形对角线的交点E,且与BC边交于点D.
如图,已知矩形OABC的两边OA、OC分别落在x轴、y轴的正半轴上,顶点B的坐标是(6,4),反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形对角线的交点E,且与BC边交于点D.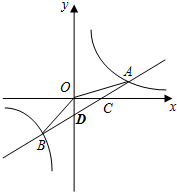 如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,与x轴交于点C,与y轴交于点D,已知OA=$\sqrt{10}$,tan∠AOC=$\frac{1}{3}$,点B的坐标为(m,-2).
如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,与x轴交于点C,与y轴交于点D,已知OA=$\sqrt{10}$,tan∠AOC=$\frac{1}{3}$,点B的坐标为(m,-2).