题目内容
20. 在菱形ABCD中,AE⊥BC于E点,CE=2,sinB=$\frac{5}{13}$,则菱形ABCD的面积为260.
在菱形ABCD中,AE⊥BC于E点,CE=2,sinB=$\frac{5}{13}$,则菱形ABCD的面积为260.
分析 利用锐角三角函数关系设AE=5x,则AB=13x,进而利用勾股定理得出x的值,再利用菱形面积求法得出答案.
解答 解:∵在菱形ABCD中,AE⊥BC于E点,CE=2,sinB=$\frac{5}{13}$,
∴设AE=5x,则AB=13x,
∴BE=13x-2,
故(13x-2)2+(5x)2=(13x)2,
解得:x1=$\frac{2}{25}$(不合题意舍去),x2=2,
∴BC=26,AE=10,
∴菱形ABCD的面积为:26×10=260.
故答案为:260.
点评 此题主要考查了菱形的性质以及勾股定理的应用,根据题意得出菱形的边长是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
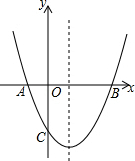 在直角坐标平面中,O为坐标原点,二次函数y=x2+bx-3的图象与x轴的负半轴交于点A,与x轴的正半轴交于点B,与y轴交于点C,且S△OAC=$\frac{3}{2}$.
在直角坐标平面中,O为坐标原点,二次函数y=x2+bx-3的图象与x轴的负半轴交于点A,与x轴的正半轴交于点B,与y轴交于点C,且S△OAC=$\frac{3}{2}$. 如图,已知△ABC中,AC=BC=6,∠C=90°,O是AB的中点,⊙O与AC、BC分别相切于点D与点E,点F是⊙O与AB的一个交点,连DF并延长交CB的延长线于点G.
如图,已知△ABC中,AC=BC=6,∠C=90°,O是AB的中点,⊙O与AC、BC分别相切于点D与点E,点F是⊙O与AB的一个交点,连DF并延长交CB的延长线于点G. 如图,设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF、再以对角线AE为边作笫三个正方形AEGH,如此下去….若正方形ABCD的边长记为a1,按上述方法所作的正方形的边长依次为a2,a3,a4,…,an,则a7=8.
如图,设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF、再以对角线AE为边作笫三个正方形AEGH,如此下去….若正方形ABCD的边长记为a1,按上述方法所作的正方形的边长依次为a2,a3,a4,…,an,则a7=8.