题目内容
9. 如图,设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF、再以对角线AE为边作笫三个正方形AEGH,如此下去….若正方形ABCD的边长记为a1,按上述方法所作的正方形的边长依次为a2,a3,a4,…,an,则a7=8.
如图,设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF、再以对角线AE为边作笫三个正方形AEGH,如此下去….若正方形ABCD的边长记为a1,按上述方法所作的正方形的边长依次为a2,a3,a4,…,an,则a7=8.
分析 根据正方形对角线等于边长的$\sqrt{2}$倍求解即可.
解答 解:由题意得,a1=1,
a2=$\sqrt{2}$a1=$\sqrt{2}$,
a3=$\sqrt{2}$a2=($\sqrt{2}$)2,
a4=$\sqrt{2}$a3=($\sqrt{2}$)3,
…,
an=$\sqrt{2}$an-1=($\sqrt{2}$)n-1.
故a7=$\sqrt{2}$a6=($\sqrt{2}$)6=8
故答案为:8.
点评 本题考查了正方形的性质,以及勾股定理在直角三角形中的运用,考查了学生找规律的能力,本题中找到an的规律是解题的关键.

练习册系列答案
相关题目
4.在长为3,4,5,12,13的线段中任意取三条可构成( ) 个直角三角形.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
14.下列每组中的两个代数式,属于同类项的是( )
| A. | $\frac{1}{2}$x2y与$\frac{2}{3}$xy2 | B. | $\frac{1}{2}$m3n与-8nm3 | C. | 3abc与3ab | D. | 0.5a2b与0.5a2c |
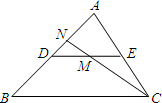 如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于点N,则S△DMN:S△DEA=1:6.
如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于点N,则S△DMN:S△DEA=1:6. 在菱形ABCD中,AE⊥BC于E点,CE=2,sinB=$\frac{5}{13}$,则菱形ABCD的面积为260.
在菱形ABCD中,AE⊥BC于E点,CE=2,sinB=$\frac{5}{13}$,则菱形ABCD的面积为260.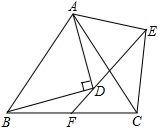 △ABC与△ADE都是以点A为顶点的等腰三角形,且∠BAC=∠DAE,BD⊥AD,ED的延长线交BC于点F,
△ABC与△ADE都是以点A为顶点的等腰三角形,且∠BAC=∠DAE,BD⊥AD,ED的延长线交BC于点F,