题目内容
下列哪一个函数，其图象与x轴有两个交点（ ）
A. y=(x-23)2+155 B. y=(x+23)2+155
C. y= -(x-23)2-155 D. y= -(x+23)2+155
D
【解析】A、令y=0得，(x-23)2+155=0，移项得，(x-23)2= -155，方程无实根；
B、令y=0得，(x+23)2+155=0，移项得，(x+23)2= -155，方程无实根；
C、令y=0得，-(x-23)2-155=0，移项得，(x-23)2= -155，方程无实根；
D、令y=0得，-(x+23)2+155=0，移项得，(x+23)2=155，方...
△ABC和△AˊBˊCˊ关于点O对称，下列结论不正确的是（ ）
A. AO=AˊO
B. AB∥AˊBˊ
C. CO=BO
D. ∠BAC=∠BˊAˊCˊ
C
【解析】因为只有对称点到对称中心的距离相等，所以C选项是错误的
故选C. 如下图，与①中的三角形相比，②中的三角形发生的变化是（ ）
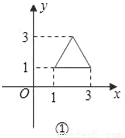
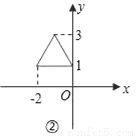
A. 向左平移3个单位 B. 向左平移2个单位
C. 向上平移3个单位 D. 向上平移1个单位
A
【解析】【解析】
由图①到图②，点（1，1）平移到点（﹣2，1），
点（3，1）平移到点（0，1），都是向左平移3个单位，
∴图形平移规律为：向左平移3个单位．
故选A． 在直角坐标系中，将点P(－3,2)向沿y轴方向向上平移4个单位长度后，得到的点坐标为( )
A. (－3,6) B. (1,2) C. (－7,2) D. (－3，－2)
A
【解析】因为点沿y轴向上移动,横坐标不变,纵坐标加上平移单位,将点P(－3,2)向沿y轴方向向上平移4个单位长度后,得到的点坐标为(－3,6),故选A. 抛物线y=2x2+4x+m与x轴只有一个公共点，则m的值为____
2
【解析】∵抛物线与x轴只有一个公共点，
∴△=0，
∴b2-4ac=42-4×2×m=0；
∴m=2．
故答案为：2. 二次函数y=ax2+bx的图象如图，若一元二次方程ax2+bx+m=0有实数根，则m的最大值为（ ）
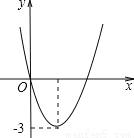
A. -3 B. 3 C. -6 D. 9
B
【解析】先根据抛物线的开口向上可知a＞0，由顶点纵坐标为-3得出b与a关系，再根据一元二次方程ax2+bx+m=0有实数根可得到关于m的不等式，求出m的取值范围即可．
【解析】
∵抛物线的开口向上，顶点纵坐标为-3，
∴a＞0， =-3，即b2=12a，
∵一元二次方程ax2+bx+m=0有实数根，
∴△=b2-4am≥0，即12a-4am≥0，即12-4m≥0，解得m≤3... 如图是二次函数y=ax2+bx+c的部分图象，由图象可知不等式ax2+bx+c＜0的解集是（ ）
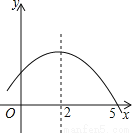
A. -1＜x＜5 B. x＞5 C. x＜-1且x＞5 D. x＜-1或x＞5
D
【解析】由图可知，抛物线的对称轴为直线x=2，与x轴的一个交点坐标为（5，0），
∴函数图象与x轴的另一交点坐标为（-1，0），
∴ax2+bx+c＜0的解集是x＜-1或x＞5．
故选C. 下列各式从左到右的变形中，是因式分解的是（ ）.
A. x（a-b）=ax-bx B. x2-1+y2=（x-1）（x+1）+y2
C. y2-1=（y+1）（y-1） D. ax+bx+c=x（a+b）+c
C
【解析】A. 是整式的乘法，故A错误；
B. 没把一个多项式转化成几个整式积，故B错误；
C. 把一个多项式转化成几个整式积，故C正确；
D. 没把一个多项式转化成几个整式积，故D错误；
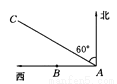
故选：C. 如图所示，某货船以20海里／时的速度将一批重要物资由A处运往正西方向的B处，经16小时到达，到达后立即卸货，此时接到气象部门通知，一台风中心正以40海里／时的速度由A处向北偏西60°的AC方向移动，距台风中心200海里的圆形区域(包括边界)均会受到影响：
(1)B处是否会受到台风的影响?清说明理由；
(2)为避免卸货过程受到台风影响，船上人员应在多少小时内卸完货物?(精确到0.1小时，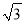 
≈1.732)
（1）B处会受到台风的影响（2）在3.9小时内卸完货才不会受台风影响
【解析】试题分析：(1)、过B作BD⊥AC于D，根据Rt△ABD的性质得出BD的长度，从而得出答案；(2)、以B为圆心，200海里为半径画圆交AC于E，F两点，连接BE，BF，根据垂径定理得出DE的长度，从而求出AE的长度，最后求出时间．
试题解析：(1)、如图所示，过B作BD⊥AC于D，在Rt△ABD中，
B...