题目内容
2.已知关于x的一元二次方程x2-(m-1)x-2(m+3)=0.(1)试证:无论m取任何实数,方程都有两个不相等的实数根;
(2)设x1、x2是方程的两根,且满足x${\;}_{1}^{2}$+x${\;}_{2}^{2}$=12,求m的值.
分析 (1)表示出根的判别式,配方后得到根的判别式大于0,进而确定出方程总有两个不相等的实数根;
(2)利用根与系数的关系可以得到x1+x2=m-1,x1•x2=-2(m+3),再把x12+x22=12进行变形可得(x1+x2)2-2x1•x2=12,然后代入计算即可求解.
解答 解:(1)∵a=1,b=m-1,c=-2(m+3),
∴△=b2-4ac=(m-1)2+4×2(m+3)=m2+6m+12=(m+3)2+3>0,
∴无论m取任何实数,方程都有两个不相等的实数根;
(2)∵x1、x2是方程的两根,
∴x1+x2=m-1,x1•x2=-2(m+3),
∵x12+x22=(x1+x2)2-2x1•x2=12,
∴(m+1)2+4(m+3)=12,
∴m2+2m+1=0,
∴m=-1.
点评 此题考查了根的判别式,根的判别式的值大于0,方程有两个不相等的实数根;根的判别式的值等于0,方程有两个相等的实数根;根的判别式的值小于0,方程没有实数根.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
14.关于x的一元二次方程x2+k=0有实数根,则( )
| A. | k<0 | B. | k>0 | C. | k≥0 | D. | k≤0 |
11.关于x的一元二次方程x2-ax=5的一个根是-1,则a的值是(( )
| A. | -1 | B. | 1 | C. | 4 | D. | -4 |
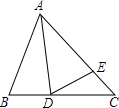 己知:如图,等边△ABC中,D、E分别是BC、AC上的点,且∠ADE=60°
己知:如图,等边△ABC中,D、E分别是BC、AC上的点,且∠ADE=60°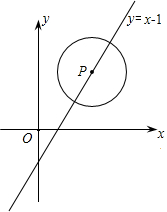 如图,已知⊙P的半径为1,圆心P在直线y=x-1的图象上运动.当⊙P与x轴相切时,则P点的坐标为(2,1)或(0,-1).
如图,已知⊙P的半径为1,圆心P在直线y=x-1的图象上运动.当⊙P与x轴相切时,则P点的坐标为(2,1)或(0,-1).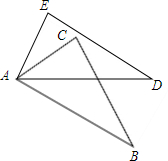 如图所示,AB=AD,AC=AE,BC=DE,如果∠EAD=70°,∠CAD=40°,求∠BAD的度数.
如图所示,AB=AD,AC=AE,BC=DE,如果∠EAD=70°,∠CAD=40°,求∠BAD的度数.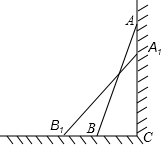 小明和同桌小聪在课后复习时,对课本“目标与评定”中的一道思考题,进行了认真地探索.思考题.如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙底端C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?
小明和同桌小聪在课后复习时,对课本“目标与评定”中的一道思考题,进行了认真地探索.思考题.如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙底端C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?