题目内容
1.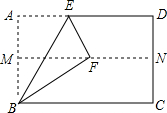 如图,在矩形ABCD中,M、N分别为边AB、CD的中点,将矩形ABCD沿BE折叠,使A点恰好落在MN上的点F处,则∠CBF的度数为( )
如图,在矩形ABCD中,M、N分别为边AB、CD的中点,将矩形ABCD沿BE折叠,使A点恰好落在MN上的点F处,则∠CBF的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 36° |
分析 根据矩形的性质及折叠的性质得出BF=2BM,从而利用含30°角的直角三角形的性质,可得出答案.
解答 解:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,AD=BC,∠BAE=∠ABC=∠D=90°,
∵M、N分别为AB、CD的中点,
∴AM=$\frac{1}{2}$AB,DN=$\frac{1}{2}$CD,
∴AM=DN,
∴四边形AMND是矩形,
∴∠BMN=90°,
由折叠的性质得:FB=AB=2BM,
∴∠BFM=30°,
∴∠FBM=60°,
∴∠CBF=30°.
故选:C.
点评 此题考查了翻折变换的知识,涉及了含30°角的直角三角形的性质、勾股定理,解答本题的关键是求出∠BFM=30°,这是解答问题的突破口.

练习册系列答案
相关题目
10. 在△ABC中,D、E为边AB、AC的中点,已知△ADE的面积为4,那么△ABC的面积是( )
在△ABC中,D、E为边AB、AC的中点,已知△ADE的面积为4,那么△ABC的面积是( )
 在△ABC中,D、E为边AB、AC的中点,已知△ADE的面积为4,那么△ABC的面积是( )
在△ABC中,D、E为边AB、AC的中点,已知△ADE的面积为4,那么△ABC的面积是( )| A. | 8 | B. | 12 | C. | 16 | D. | 20 |
6.两条抛物线y1=-$\frac{1}{2}$x2+b,y2=-$\frac{1}{2}$x2-b与分别经过点(-2,0),(2,0)且平行于y轴的两条平行线围成的部分的面积为8,则b等于( )
| A. | 1 | B. | -3 | C. | 4 | D. | -1或3 |
11.下列运算中正确的是( )
| A. | (a-b)2=a2-b2 | B. | (-a+1)(-a-1)=a2-1 | C. | (-$\frac{1}{2}$)-2=1 | D. | -(-2ab2)2=4a2b4 |
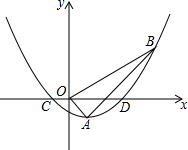 如图,在平面直角坐标系中,顶点为A(1,-1)的抛物线经过点B(5,3),且与x轴交于C,D两点(点C在点D的左侧).
如图,在平面直角坐标系中,顶点为A(1,-1)的抛物线经过点B(5,3),且与x轴交于C,D两点(点C在点D的左侧).

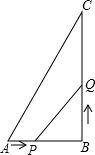 如图所示,在△ABC中∠B=90°,AB=6cm,BC=8cm,点P从点A开始沿AB边向点B以1cm/s的速度运动,点Q从点B开始沿BC边向点C以2cm/s的速度运动.
如图所示,在△ABC中∠B=90°,AB=6cm,BC=8cm,点P从点A开始沿AB边向点B以1cm/s的速度运动,点Q从点B开始沿BC边向点C以2cm/s的速度运动.