题目内容
1.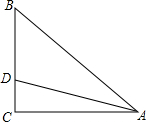 如图,在Rt△ABC中,∠C=90°,AB=10,tanB=$\frac{4}{3}$,CD=2,求△ABD的周长.
如图,在Rt△ABC中,∠C=90°,AB=10,tanB=$\frac{4}{3}$,CD=2,求△ABD的周长.
分析 先解Rt△ABC,由∠C=90°,tanB=$\frac{AC}{BC}$=$\frac{4}{3}$,AB=10,利用勾股定理可得AC=8,BC=6.再解Rt△ADC,利用勾股定理求出AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=2$\sqrt{17}$,进而得到△ABD的周长=AB+BD+AD=14+2$\sqrt{17}$.
解答 解:∵在Rt△ABC中,∠C=90°,
∴tanB=$\frac{AC}{BC}$=$\frac{4}{3}$,
∴可设AC=4k,则BC=3k,
由勾股定理得AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{(4k)^{2}+(3k)^{2}}$=5k,
∵AB=10,
∴5k=10,k=2,
∴AC=8,BC=6.
∵在Rt△ADC中,∠C=90°,AC=8,CD=2,
∴AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=$\sqrt{{8}^{2}+{2}^{2}}$=2$\sqrt{17}$.
∵BC=6,CD=2,
∴BD=BC-CD=6-2=4,
∴△ABD的周长=AB+BD+AD=10+4+2$\sqrt{17}$=14+2$\sqrt{17}$.
点评 本题考查了解直角三角形,锐角三角函数的定义,勾股定理,三角形的周长,求出AC=8,BC=6是解题的关键.

练习册系列答案
相关题目
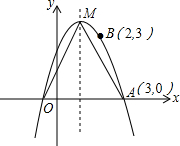 如图,已知抛物线y=-x2+bx+c过点A(3,0)、B(2,3),其顶点为M.
如图,已知抛物线y=-x2+bx+c过点A(3,0)、B(2,3),其顶点为M. 如图,搭一个小正方形需要4根火柴棒,搭2个小正方形需要7根火柴棒,…搭70个小正方形,需要211个火柴棒.
如图,搭一个小正方形需要4根火柴棒,搭2个小正方形需要7根火柴棒,…搭70个小正方形,需要211个火柴棒.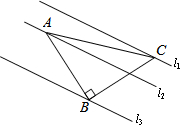 如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为7,l2,l3之间的距离为8,求AC的长.
如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为7,l2,l3之间的距离为8,求AC的长.