题目内容
7.已知(ab-2)2+|b-1|=0,求$\frac{1}{ab}$+$\frac{1}{(a+1)(b+1)}$+$\frac{1}{(a+2)(b+2)}$+…+$\frac{1}{(a+2014)(b+2014)}$.分析 先根据非负数的性质求出a、b的值,再代入代数式进行计算即可.
解答 解:∵(ab-2)2+|b-1|=0,
∴ab-2=0,b-1=0,解得a=2,b=1,
∴原式=$\frac{1}{2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{20015×2016}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2015}$-$\frac{1}{2016}$
=1-$\frac{1}{2016}$
=$\frac{2015}{2016}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.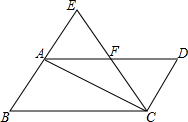 如图,在平行四边形ABCD中,∠B=60°,将△ABC沿对角线AC折叠,点B的对应点落在点E处,且点B,A,E在一条直线上,CE交AD于点F,则图中等边三角形共有( )
如图,在平行四边形ABCD中,∠B=60°,将△ABC沿对角线AC折叠,点B的对应点落在点E处,且点B,A,E在一条直线上,CE交AD于点F,则图中等边三角形共有( )
 如图,在平行四边形ABCD中,∠B=60°,将△ABC沿对角线AC折叠,点B的对应点落在点E处,且点B,A,E在一条直线上,CE交AD于点F,则图中等边三角形共有( )
如图,在平行四边形ABCD中,∠B=60°,将△ABC沿对角线AC折叠,点B的对应点落在点E处,且点B,A,E在一条直线上,CE交AD于点F,则图中等边三角形共有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
16.$\sqrt{2}$的相反数是( )
| A. | -$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |