题目内容
19.我国铁路实现了第六次大提速,给旅客的出行带来了很大的方便.例如,京沪线全长约1500公里,第六次提速后,特快列车运行全程所用时间比第五次提速后少用1$\frac{7}{8}$小时.已知第六次提速后与第五次提速后的平均时速比为5:4.求第五次提速后和第六次提速后的平均时速各是多少?分析 根据关键描述语是特快列车运行全程所用时间比第五次提速后少用$\frac{7}{8}$小时,可得等量关系为:第5次提速所用时间-第6次提速所用时间=1$\frac{7}{8}$.
解答 解:设第五次提速后的平均速度是x公里/时,则第六次提速后的平均速度是(x+40)公里/时.
根据题意,得:$\frac{1500}{4x}$-$\frac{1500}{5x}$=1$\frac{7}{8}$,
解之得:x=40,
经检验,x=40是原方程的解.
则4x=160,5x=200.
答:第五次提速后的平均时速为160公里/时,第六次提速后的平均时速为200公里/时.
点评 本题考查分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.

练习册系列答案
相关题目
7.下列各组向量中,是平行向量的一组是( )
| A. | $\overrightarrow{a}$$+\overrightarrow{b}$与$\frac{1}{2}$$\overrightarrow{a}$$+\overrightarrow{b}$$-\frac{1}{2}$$\overrightarrow{b}$ | B. | $\frac{1}{2}$($\overrightarrow{a}$$-3\overrightarrow{b}$)与$\frac{3}{2}$($\overrightarrow{a}$$-2\overrightarrow{b}$) | C. | 2$\overrightarrow{a}$$+\overrightarrow{b}$与$\overrightarrow{a}$$+\overrightarrow{b}$ | D. | 5$\overrightarrow{a}$$-3\overrightarrow{b}$与$\frac{2}{3}$$\overrightarrow{a}$$-\frac{1}{5}$$\overrightarrow{b}$ |
14.若分式$\frac{{x}^{2}-4}{x-2}$的值为0,则x的取值为( )
| A. | x=2 | B. | x=-2 | C. | x=2 | D. | 无法确定 |
4.抛物线y=ax2+bx+c经过点A(-1,2),B(1,-2),则b的值为( )
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
8.“a与b的$\frac{1}{10}$的差”,用代数式表示为( )
| A. | $\frac{1}{10}$(a-b) | B. | a-$\frac{1}{10}$b | C. | a+b-$\frac{1}{10}$ | D. | a-b-$\frac{1}{10}$ |
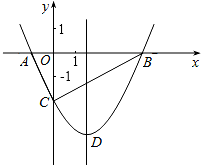 如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A,B两点,与y轴交于C点,且A(-1,0).
如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A,B两点,与y轴交于C点,且A(-1,0).