题目内容
12.一个角的两边与另一个角的两边分别垂直,则这两个角的关系是( )| A. | 相等 | B. | 互补 | C. | 互余 | D. | 相等或互补 |
分析 此题可以通过两个图形得出这两个角的关系相等或互补.
解答 
 解:如图:
解:如图:
图1中,根据垂直的量相等的角都等于90°,对顶角相等,
所以∠1=∠2,
图2中,同样根据垂直的量相等的角都等于90°,根据四边形的内角和等于360°,
所以∠1+∠2=360°-90°-90°=180°,
∴如果一个角的两边与另一个角的两边分别垂直,那么这两个角的关系是相等或互补,
故选D.
点评 此题考查的知识点是垂直,关键明确四边形的内角和等于360°,三角形的内角和等于180°,对顶角相等的性质,对图形准确分析利用是解题的关键.

练习册系列答案
相关题目
2.下列各式中,无意义的是( )
| A. | -$\sqrt{2}$ | B. | $\sqrt{-2}$ | C. | $\sqrt{(-2)^2}$ | D. | ±$\sqrt{2}$ |
7.下列各式成立的是( )
| A. | $\sqrt{{a}^{2}}$=a | B. | $\sqrt{(-3)^{2}}$=-3 | C. | $\sqrt{(-3)^{2}}$=±3 | D. | $\sqrt{(-3)^{2}}$=3 |
17.下列各式计算正确的是( )
| A. | 2$\sqrt{3}$+4$\sqrt{2}$=6$\sqrt{5}$ | B. | $\sqrt{27}$÷$\sqrt{3}$=3 | C. | 3$\sqrt{3}$+3$\sqrt{2}$=3$\sqrt{6}$ | D. | $\sqrt{(-5)^{2}}$=-5 |
1.已知关于x的方程mx2+(m+1)x+2=0的两根一个大于1,另一个小于1,则实数m的取值范围是( )
| A. | -$\frac{3}{2}$<m<0 | B. | m<$-\frac{3}{2}$或m>0 | C. | m<0 | D. | m>$-\frac{3}{2}$ |
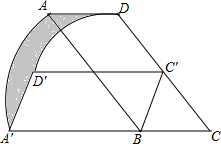 如图,在?ABCD中,∠BCD=60°,AB=2BC=4,将?ABCD绕点B逆时针旋转一定角度后得到?A′BC′D′,其中点C的对应点C′落在边CD上,则图中阴影部分的面积.
如图,在?ABCD中,∠BCD=60°,AB=2BC=4,将?ABCD绕点B逆时针旋转一定角度后得到?A′BC′D′,其中点C的对应点C′落在边CD上,则图中阴影部分的面积.