题目内容
20.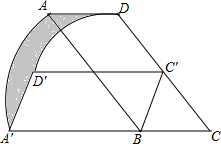 如图,在?ABCD中,∠BCD=60°,AB=2BC=4,将?ABCD绕点B逆时针旋转一定角度后得到?A′BC′D′,其中点C的对应点C′落在边CD上,则图中阴影部分的面积.
如图,在?ABCD中,∠BCD=60°,AB=2BC=4,将?ABCD绕点B逆时针旋转一定角度后得到?A′BC′D′,其中点C的对应点C′落在边CD上,则图中阴影部分的面积.
分析 由旋转可得CB=C′B,根据∠C=60°可得△BCC′为等边三角形、△BCD为直角三角形,继而可得旋转角∠ABA′=∠DBD′=∠CBC′=60°,BD=2$\sqrt{3}$,最后根据阴影部分的面积=S扇形BAA′-S扇形BDD′计算可得.
解答 解:如图,连接BD、BD′,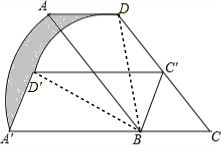
∵?A′BC′D′是由?ABCD绕点B旋转得到的,
∴∠ABA′=∠CBC′=∠DBD′,AB=A′B,CB=C′B,BD=BD′,
∵∠BCD=60°,AB=2BC=4,
∴BC′=BC=2=$\frac{1}{2}$AB=$\frac{1}{2}$CD,
∴△BCD是直角三角形,∠ABA′=∠CBC′=∠DBD′=60°,
∴BD=$\sqrt{C{D}^{2}-B{C}^{2}}$=2$\sqrt{3}$,
则阴影部分的面积=S扇形BAA′-S扇形BDD′
=$\frac{60•π•{4}^{2}}{360}$-$\frac{60•π•(2\sqrt{3})^{2}}{360}$
=$\frac{2}{3}$π.
点评 本题主要考查旋转的性质、平行四边形的性质、勾股定理、等边三角形等知识点,根据已知条件求得旋转半径和旋转角是求扇形面积的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
10.下列各式计算正确的是( )
| A. | $\sqrt{4}$=±2 | B. | $\sqrt{5}$-$\sqrt{3}$=$\sqrt{2}$ | C. | $\sqrt{2}$×$\sqrt{5}$=$\sqrt{10}$ | D. | $\sqrt{12}$÷2=$\sqrt{6}$ |
8.下列说法正确的是( )
| A. | $\sqrt{9}$的平方根是±3 | B. | -a2一定没有平方根 | ||
| C. | 0.9的平方根是±0.3 | D. | a2+1一定有平方根 |
15.下列叙述正确的是( )
| A. | -8的立方根是-2 | B. | 0.4的平方根是±0.2 | ||
| C. | -(-3)2的立方根不存在 | D. | ±4是16的算术平方根 |
5.下面说法正确的是( )
| A. | $\frac{1}{4}$和-4互为相反数 | B. | $\frac{1}{4}$和-4互为倒数 | ||
| C. | 0.1和10互为倒数 | D. | 0的倒数是0 |
12.一个角的两边与另一个角的两边分别垂直,则这两个角的关系是( )
| A. | 相等 | B. | 互补 | C. | 互余 | D. | 相等或互补 |
10.将平面直角坐标系中的点A(2,1)向左平移2个单位长度,再向下平移4个单位长度得到点A′,若将点A到A′的平移看作一次平移,则平移的距离为( )
| A. | 6个单位长度 | B. | 4个单位长度 | C. | 2个单位长度 | D. | 2$\sqrt{5}$个单位长度 |
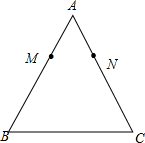 (1)下列仅用无刻度的直尺就能完成作图的是②(填写序号即可)
(1)下列仅用无刻度的直尺就能完成作图的是②(填写序号即可)