题目内容
1.已知关于x的方程mx2+(m+1)x+2=0的两根一个大于1,另一个小于1,则实数m的取值范围是( )| A. | -$\frac{3}{2}$<m<0 | B. | m<$-\frac{3}{2}$或m>0 | C. | m<0 | D. | m>$-\frac{3}{2}$ |
分析 构造函数f(x)=mx2+(m+1)x+2,根据二次函数性质分m>0时f(1)>0和m<0时f(1)<0分别求得m的范围.
解答 解:设f(x)=mx2+(m+1)x+2,要使方程的两根一个大于1,另一个小于1,
则当m>0时,f(1)=m+m+1+2>0,解得:m>-$\frac{3}{2}$,
故m>0;
当m<0时,f(1)=m+m+1+2<0,解得:m<-$\frac{3}{2}$,
故m<-$\frac{3}{2}$,
综上,m<-$\frac{3}{2}$或m>0,
故选:B.
点评 本题主要考查一元二次方程根与系数的关系,解题的关键是建立函数,利用函数的思想解决方程的问题.

练习册系列答案
相关题目
12.一个角的两边与另一个角的两边分别垂直,则这两个角的关系是( )
| A. | 相等 | B. | 互补 | C. | 互余 | D. | 相等或互补 |
16.下面的计算正确的是( )
| A. | m3+m3=m6 | B. | m3•m3=2m3 | C. | m3•m=m3 | D. | -m3•(-m3)=m6 |
6.已知一元二次方程x2+3x+2=0,下列判断正确的是( )
| A. | 该方程无实数解 | B. | 该方程有两个相等的实数解 | ||
| C. | 该方程有两个不相等的实数解 | D. | 该方程解的情况不确定 |
10.将平面直角坐标系中的点A(2,1)向左平移2个单位长度,再向下平移4个单位长度得到点A′,若将点A到A′的平移看作一次平移,则平移的距离为( )
| A. | 6个单位长度 | B. | 4个单位长度 | C. | 2个单位长度 | D. | 2$\sqrt{5}$个单位长度 |
11.不等式3x≤6的解集是( )
| A. | x≤$\frac{1}{2}$ | B. | x≥$\frac{1}{2}$ | C. | x≤2 | D. | x≥2 |
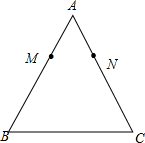 (1)下列仅用无刻度的直尺就能完成作图的是②(填写序号即可)
(1)下列仅用无刻度的直尺就能完成作图的是②(填写序号即可)