题目内容
3.若分解因式x2+mx-24=(x+3)(x+n),则m的值为-5.分析 已知等式右边利用多项式乘以多项式法则计算,再利用多项式相等的条件求出m的值即可.
解答 解:已知等式整理得:x2+mx-24=(x+3)(x+n)=x2+(n+3)x+3n,
可得m=n+3,3n=-24,
解得:m=-5,n=-8,
故答案为:-5.
点评 此题考查了因式分解-十字相乘法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
2.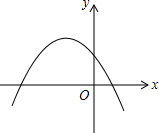 已知抛物线y=ax2+bx+c的图象如图所示,则直线y=ax-b一定不经过( )
已知抛物线y=ax2+bx+c的图象如图所示,则直线y=ax-b一定不经过( )
 已知抛物线y=ax2+bx+c的图象如图所示,则直线y=ax-b一定不经过( )
已知抛物线y=ax2+bx+c的图象如图所示,则直线y=ax-b一定不经过( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
8.一次函数y=(3m-2)x+2m-1的图象交于y轴的正半轴,则m的取值范围是( )
| A. | m>$\frac{2}{3}$ | B. | m>$\frac{1}{2}$ | C. | m<$\frac{1}{2}$ | D. | m<$\frac{2}{3}$ |
12.下列运算正确的是( )
| A. | $\sqrt{2016}$+$\sqrt{2016}$=$\sqrt{4032}$ | B. | $\sqrt{201{6}^{2}-(\frac{1}{2016})^{2}}=2016-\frac{1}{2016}$ | ||
| C. | $\sqrt{2016}×\sqrt{4032}$=2016$\sqrt{2}$ | D. | $\sqrt{2016}÷\sqrt{2}=1008$ |
13. 如图,正方形ABCD中,AE垂直于BE,且AE=6,BE=8,则阴影部分的面积是( )
如图,正方形ABCD中,AE垂直于BE,且AE=6,BE=8,则阴影部分的面积是( )
 如图,正方形ABCD中,AE垂直于BE,且AE=6,BE=8,则阴影部分的面积是( )
如图,正方形ABCD中,AE垂直于BE,且AE=6,BE=8,则阴影部分的面积是( )| A. | 64 | B. | 72 | C. | 76 | D. | 84 |
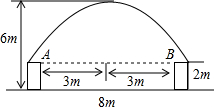 某一隧道内设双行线公路,其截面由一长方形和一抛物线构成,如图所示,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5m,若行车道总宽度AB为6m,请计算车辆经过隧道时的限制高度是多少米?(精确到0.1m)
某一隧道内设双行线公路,其截面由一长方形和一抛物线构成,如图所示,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5m,若行车道总宽度AB为6m,请计算车辆经过隧道时的限制高度是多少米?(精确到0.1m)