题目内容
如图,在数轴上的A1、A2、A3、A4…A20,这20个点所表示的数分别为a1、a2、a3、a4、…a20.若A1A2=A2A3=…=A19A20,且a3=20,|a1-a4|=12.
(1)求a1的值;
(2)若|a1-x|=a2+a4,求x的值;
(3)求a20的值.

(1)求a1的值;
(2)若|a1-x|=a2+a4,求x的值;
(3)求a20的值.

考点:一元一次方程的应用,数轴
专题:
分析:(1)设A1A2=A2A3=…=A19A20=m,由|a1-a4|=12建立方程求出m的值结合图形就可以求出结论;
(2)由a1的可以求出a2、a4的值,再解关于绝对值的方程就可以求出结论;
(3)由图形可以得出an=a1+4(n-1)就可以求出a20的值.
(2)由a1的可以求出a2、a4的值,再解关于绝对值的方程就可以求出结论;
(3)由图形可以得出an=a1+4(n-1)就可以求出a20的值.
解答:解:(1)设A1A2=A2A3=…=A19A20=m,由题意,得
3m=12,
解得m=4,
∵a1=a3-2m,且a3=20,
∴a1=20-2×4=12.
答:a1的值为12;
(2)∵a1=12,m=4,
∴a2=16,a4=24,
∴|12-x|=16+24
∴12-x=±40,
∴x=-28或52.
答:x的值为-28或52;
(3)∵a1=12,a2=16,a3=20,
∴an=a1+4(n-1).
当n=20时,a20=12+4×(20-1)=88.
答:a20的值为88.
3m=12,
解得m=4,
∵a1=a3-2m,且a3=20,
∴a1=20-2×4=12.
答:a1的值为12;
(2)∵a1=12,m=4,
∴a2=16,a4=24,
∴|12-x|=16+24
∴12-x=±40,
∴x=-28或52.
答:x的值为-28或52;
(3)∵a1=12,a2=16,a3=20,
∴an=a1+4(n-1).
当n=20时,a20=12+4×(20-1)=88.
答:a20的值为88.
点评:本题考查了数轴上两点间的距离公式的运用,含绝对值的一元一次方程的解法及运用,探究规律试题的运用,解答时由数轴上两点间的距离公式求出数轴上的点表示的数是关键.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
抛物线y=x2+2x+3绕着它的顶点旋转180°,则旋转之后的抛物线解析式是( )
| A、y=-x2-2x-3 |
| B、y=-x2-x+1 |
| C、y=-x2-2x+1 |
| D、y=-x2-2x-1 |
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①abc>0;②a+b+c=0;③a>
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①abc>0;②a+b+c=0;③a> 在梯形ABCD中,AD∥BC,AB=AD+BC,E为CD中点,∠BAE=55°,则∠EBC=
在梯形ABCD中,AD∥BC,AB=AD+BC,E为CD中点,∠BAE=55°,则∠EBC=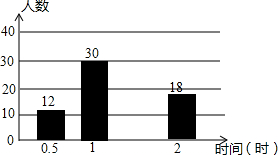 在济南市开展的“美丽泉城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
在济南市开展的“美丽泉城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示: