题目内容
已知一元二次方程x2+x+n-
=0有两个相等的实数根,另一个一元二次方程nx2-2(m-1)x+m2-4m+6=0有两个不相等的整数根,且m是小于5的整数,求m和n的值.
| 3 |
| 4 |
考点:根的判别式
专题:计算题
分析:先根据一元二次方程x2+x+n-
=0有两个相等的实数根,利用判别式的意义得到1-4×(n-
)=0,可求得n=1;再根据x2-2(m-1)x+m2-4m+6=0有两个不相等的整数根,利用判别式的意义得到△=4(m-1)2-4(m2-4m+6)>0,解得m>
,然后找出
<m<5中的整数即可得到m的值.
| 3 |
| 4 |
| 3 |
| 4 |
| 5 |
| 2 |
| 5 |
| 2 |
解答:解:根据题意得1-4×(n-
)=0,解得n=1,
而x2-2(m-1)x+m2-4m+6=0有两个不相等的整数根,
所以△=4(m-1)2-4(m2-4m+6)=8m-20>0,解得m>
,
因为m是小于5的整数,
所以m的值为3或4.
| 3 |
| 4 |
而x2-2(m-1)x+m2-4m+6=0有两个不相等的整数根,
所以△=4(m-1)2-4(m2-4m+6)=8m-20>0,解得m>
| 5 |
| 2 |
因为m是小于5的整数,
所以m的值为3或4.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
已知实数ab满足(a2+b2-1)(a2+b2+3)=12,那么( )
| A、a2+b2=3 |
| B、a2+b2=-5 |
| C、a2+b2=3或a2+b2=5 |
| D、a2+b2=2 |
 下列四个三角形,与如图的三角形相似的是( )
下列四个三角形,与如图的三角形相似的是( )A、 |
B、 |
C、 |
D、 |
 (1)如图,小红同学用仪器测量一棵大树AB的高度,在C处测得∠ADG=30°,在E处测得∠AFG=60°,CE=8米,仪器高度CD=1.5米,求这棵树AB的高度(结果保留两位有效数字,
(1)如图,小红同学用仪器测量一棵大树AB的高度,在C处测得∠ADG=30°,在E处测得∠AFG=60°,CE=8米,仪器高度CD=1.5米,求这棵树AB的高度(结果保留两位有效数字,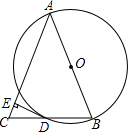 如图,以等腰△ABC中的腰AB为直径作⊙O,交底边BC于点D.过点D作DE⊥AC,垂足为E.
如图,以等腰△ABC中的腰AB为直径作⊙O,交底边BC于点D.过点D作DE⊥AC,垂足为E.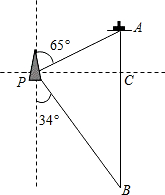 如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处离灯塔P有多远(结果保留小数点后一位)
如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处离灯塔P有多远(结果保留小数点后一位)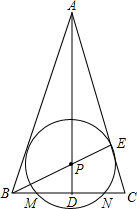 已知△ABC,AB=AC,∠BAC=30°,AD⊥BC于D,E在AC上,BE=BC,BC=2
已知△ABC,AB=AC,∠BAC=30°,AD⊥BC于D,E在AC上,BE=BC,BC=2