题目内容
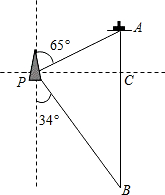如图，一艘海轮位于灯塔P的北偏东65°方向，距离灯塔80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东34°方向上的B处，这时，海轮所在的B处离灯塔P有多远（结果保留小数点后一位）考点：解直角三角形的应用-方向角问题
专题：
分析：首先求出PC的长，再利用PB=
进而得出答案．
| PC |
| sin∠B |
解答：解：如图，在Rt△APC中，∠APC=90°-65°=25°，
∴PC=PA•cos∠APC≈80×0.91=72.8（海里），
在Rt△BPC中，∠B=34°，
则PB=
=
=130（海里）
答：海轮所在的B处距离灯塔P约有130海里．
解：如图，在Rt△APC中，∠APC=90°-65°=25°，∴PC=PA•cos∠APC≈80×0.91=72.8（海里），
在Rt△BPC中，∠B=34°，
则PB=
| PC |
| sin∠B |
| 72.8 |
| 0.56 |
答：海轮所在的B处距离灯塔P约有130海里．
点评：此题主要考查了解直角三角形的应用，利用锐角三角函数关系得出PC长是解题关键．
练习册系列答案
相关题目
关于x的一元二次方程x2+px-6=0的一个根为2，则p的值为（ ）
| A、-2 | B、2 | C、-1 | D、1 |
如图，已知∠ABE+∠E+∠CDE=360°，证明：AB∥CD．