题目内容
10.若直线y=k1x+1与y=k2x-4的交点在x轴上,那么$\frac{k_1}{k_2}$等于( )| A. | 4 | B. | -4 | C. | $\frac{1}{4}$ | D. | $-\frac{1}{4}$ |
分析 分别求出两直线与x轴的交点的横坐标,然后列出方程整理即可得解.
解答 解:令y=0,则k1x+1=0,
解得x=-$\frac{1}{{k}_{1}}$,
k2x-4=0,
解得x=$\frac{4}{{k}_{2}}$,
∵两直线交点在x轴上,
∴-$\frac{1}{{k}_{1}}$=$\frac{4}{{k}_{2}}$,
∴$\frac{k_1}{k_2}$=-$\frac{1}{4}$.
故选:D.
点评 本题考查了两直线相交的问题,分别表示出两直线与x轴的交点的横坐标是解题的关键.

练习册系列答案
相关题目
20.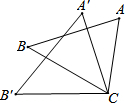 如图,△ACB≌△A′B′C′,AC与A′C,是对应边,∠A=60°,∠ACB=70°,则∠B′的度数为( )
如图,△ACB≌△A′B′C′,AC与A′C,是对应边,∠A=60°,∠ACB=70°,则∠B′的度数为( )
 如图,△ACB≌△A′B′C′,AC与A′C,是对应边,∠A=60°,∠ACB=70°,则∠B′的度数为( )
如图,△ACB≌△A′B′C′,AC与A′C,是对应边,∠A=60°,∠ACB=70°,则∠B′的度数为( )| A. | 70° | B. | 60° | C. | 50° | D. | 40° |
2.下列运算正确的是( )
| A. | 3a2+5a2=8a4 | B. | 5a+7b=12ab | C. | 2m2n-5nm2=-3m2n | D. | 2a-2a=a |
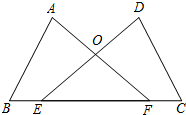 如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.


