题目内容
18.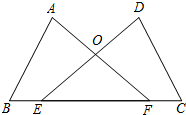 如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.(1)求证:△ABF≌△DCE;
(2)过O点作OM⊥BC,垂足为M,试判断线段OE与OF的大小关系,并说明理由.
分析 (1)利用等式的性质可以证得BF=CE,则依据AAS即可证得三角形全等;
(2)依据全等三角形的性质,即可证得∠AFB=∠DEC,然后依据等角对等边从而证得.
解答 (1)证明:∵BE=CF,
∴BE+EF=CF+EF,即BF=CE,
∵在△ABF和△DCE中,
$\left\{\begin{array}{l}{∠A=∠D}\\{∠B=∠C}\\{BF=CE}\end{array}\right.$,
∴△ABF≌△DCE(AAS);
(2)∵△ABF≌△DCE,
∴∠AFB=∠DEC,
∴OE=OF.
点评 本题考查了全等三角形的判定与性质,以及等腰三角形的判定定理:等角对等边,正确证明两个三角形全等是关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
13.如果(x+2)(x-6)=x2+px+q,则p、q的值为( )
| A. | p=-4,q=-12 | B. | p=4,q=-12 | C. | p=-8,q=-12 | D. | p=8,q=12 |
10.若直线y=k1x+1与y=k2x-4的交点在x轴上,那么$\frac{k_1}{k_2}$等于( )
| A. | 4 | B. | -4 | C. | $\frac{1}{4}$ | D. | $-\frac{1}{4}$ |
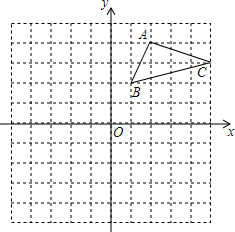 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,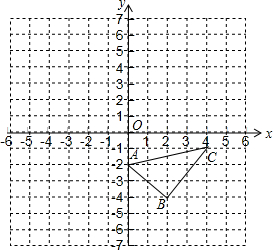 如图,已知△ABC,
如图,已知△ABC,