Question

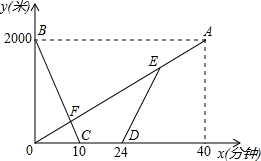甲、乙两地之间有一条笔直的公路L，小明从甲地出发沿公路L步行前往乙地，同时小亮从乙地出发沿公路L骑自行车前往甲地，小亮到达甲地停留一段时间，按原路原速返回，追上小明后两人一起步行到乙地．如图，线段OA表示小明与甲地的距离为y₁（米）与行走的时间为x（分钟）之间的函数关系；折线BCDEA表示小亮与甲地的距离为y₂（米）与行走的时间为x（分钟）之间的函数关系．请根据图象解答下列问题：
（1）小明步行的速度是

 

米/分钟，小亮骑自行车的速度

 

米/分钟；
（2）图中点F坐标是（

 

，

 

）、点E坐标是（

 

，

 

）；
（3）求y₁、y₂与x之间的函数关系式；
（4）请直接写出小亮从乙地出发再回到乙地过程中，经过几分钟与小明相距300米？

Answer 1

考点：一次函数的应用

专题：

分析：（1）根据图象可知小明步行的速度是2000÷40=50米/分钟，小亮骑自行车的速度2000÷10=200米/分钟；
（2）（3）分别设小明、小亮与甲地的距离为y₁（米）、y₂（米）与x（分钟）之间的函数关系式为y₁=k₁x，y₂=k₂x+b，由待定系数法根据图象就可以求出解析式；再进一步求得交点的坐标，得出点F、E的坐标即可；
（4）分追击问题与相遇的过程中小亮与小明相距300米探讨得出答案即可．

解答：解：（1）小明步行的速度是2000÷40=50米/分钟，小亮骑自行车的速度2000÷10=200米/分钟；
（2）设小明与甲地的距离为y₁（米）与x（分钟）之间的函数关系式为y₁=k₁x，
代入点（40，2000）得：2000=40k₁，解得k₁=50，
所以y₁=50x，
设小亮与甲地的距离为y₂（米）与x（分钟）之间的函数关系式为y₂=k₂x+b，
则代入点（0，2000）和（10，0）得

b=2000 k2=-200

，
所以y_BC=-200x+2000，
由图可知24分钟时两人的距离为：S=24×50=1200，
小亮从甲地追上小明的时间为24×50÷（200-50）=8分钟，
也就是32分钟时为0，则y₁=50x=1600，则点E坐标为（32，1600）；
由题意得

y=50x y=-200x+2000

，
解得

x=8 y=400

，
所以图中点F坐标是（8，400）；
（3）由（2）可知y₁=50x，
y_BC=-200x+2000（0≤x≤10），
设S与x之间的函数关系式为：S=kx+b，由题意，

24k+b=1200 32k+b=0

，
解得：

k=-150 b=4800

，
∴S=-150x+4800，
即y_ED=-150x+4800（24≤x≤32）；
（4）当0≤x≤10时，
（2000-300）÷（50+200）=6.8（分钟）
当8≤x≤10，
300÷（50+200）+8=9.2（分钟）
当24≤x≤32，
则50x-（-150x+4800）=300，
解得x=25.5（分钟）
答：小亮从乙地出发再回到乙地过程中，经过6.8分钟，9.2分钟，25.5分钟时与小明相距300米．

点评：此题考查一次函数的实际运用，注意利用待定系数法求函数解析式，以及分类讨论思想的渗透．