题目内容
 如图,已知P是正方形ABCD内一点,PA=1,PB=2,PC=3,以点B为旋转中心,将△ABP沿顺时针方向旋转,使点A与点C重合,这时P点旋转到G点,连接BG、CG、PG.
如图,已知P是正方形ABCD内一点,PA=1,PB=2,PC=3,以点B为旋转中心,将△ABP沿顺时针方向旋转,使点A与点C重合,这时P点旋转到G点,连接BG、CG、PG.(1)△ABP以点B为旋转中心旋转了
(2)求出PG的长度;
(3)以点G为圆心,r为半径作⊙G:
①当半径r满足
②当半径r满足
③当半径r满足
考点:几何变换综合题
专题:
分析:(1)根据正方形性质和旋转的性质得出即可;
(2)先根据旋转得出直角三角形,再根据勾股定理求出即可;
(3)先求出三角形PGC的高GE的长,再根据直线和圆的位置关系得出即可.
(2)先根据旋转得出直角三角形,再根据勾股定理求出即可;
(3)先求出三角形PGC的高GE的长,再根据直线和圆的位置关系得出即可.
解答:解:(1)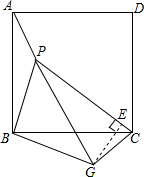
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∵以点B为旋转中心,将△ABP沿顺时针方向旋转,使点A与点C重合,
∴△ABP以点B为旋转中心旋转了90°,
故答案为:90;
(2)∵△ABP绕B顺时针旋转90°到△BGC,
∴∠PBG=90°,BP=BG=2,AP=CG=1,
∴由勾股定理得:PG=
=2
;
(3)过G作GE⊥PC于E,
∵PC=3,PG=2
,CG=1,
∴PC2=PG2+CG2,
∴∠PGC=90°,
根据三角形的面积公式得:PC×DE=PG×CG,
∴3×DE=2
×1,
∴DE=
,
∵PG=2
,CG=1,
∴①当半径r=
或1时,⊙G与边PC只有一个交点;
②当半径r满足
<r≤1时,⊙G与边PC有两个交点;
③当半径r满足r<
或r>2
时,⊙G与边PC没有交点;
故答案为:=
或2
,
<r≤1,r<
或r>2
.

∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∵以点B为旋转中心,将△ABP沿顺时针方向旋转,使点A与点C重合,
∴△ABP以点B为旋转中心旋转了90°,
故答案为:90;
(2)∵△ABP绕B顺时针旋转90°到△BGC,
∴∠PBG=90°,BP=BG=2,AP=CG=1,
∴由勾股定理得:PG=
| 22+22 |
| 2 |
(3)过G作GE⊥PC于E,
∵PC=3,PG=2
| 2 |
∴PC2=PG2+CG2,
∴∠PGC=90°,
根据三角形的面积公式得:PC×DE=PG×CG,
∴3×DE=2
| 2 |
∴DE=
2
| ||
| 3 |
∵PG=2
| 2 |
∴①当半径r=
2
| ||
| 3 |
②当半径r满足
2
| ||
| 3 |
③当半径r满足r<
2
| ||
| 3 |
| 2 |
故答案为:=
2
| ||
| 3 |
| 2 |
2
| ||
| 3 |
2
| ||
| 3 |
| 2 |
点评:本题考查了直线和圆的位置关系,正方形的性质,三角形的面积,旋转的性质,勾股定理,勾股定理的逆定理的应用,题目综合性比较强,难度偏大.

练习册系列答案
相关题目
 如图,在四边形ABCD中,AB=AD=2,∠A=60°,BC=2
如图,在四边形ABCD中,AB=AD=2,∠A=60°,BC=2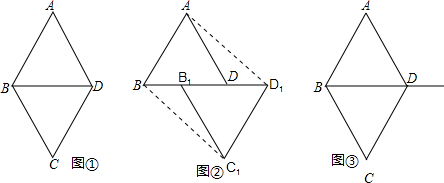
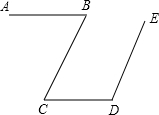 结合图形,把下列解答过程补充完整.
结合图形,把下列解答过程补充完整.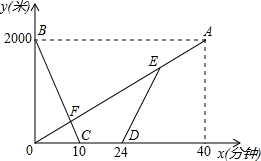 甲、乙两地之间有一条笔直的公路L,小明从甲地出发沿公路L步行前往乙地,同时小亮从乙地出发沿公路L骑自行车前往甲地,小亮到达甲地停留一段时间,按原路原速返回,追上小明后两人一起步行到乙地.如图,线段OA表示小明与甲地的距离为y1(米)与行走的时间为x(分钟)之间的函数关系;折线BCDEA表示小亮与甲地的距离为y2(米)与行走的时间为x(分钟)之间的函数关系.请根据图象解答下列问题:
甲、乙两地之间有一条笔直的公路L,小明从甲地出发沿公路L步行前往乙地,同时小亮从乙地出发沿公路L骑自行车前往甲地,小亮到达甲地停留一段时间,按原路原速返回,追上小明后两人一起步行到乙地.如图,线段OA表示小明与甲地的距离为y1(米)与行走的时间为x(分钟)之间的函数关系;折线BCDEA表示小亮与甲地的距离为y2(米)与行走的时间为x(分钟)之间的函数关系.请根据图象解答下列问题: